题目内容
甲、乙两车在A、B两城不断来回开行,两车的速度不等,且均为匀速(忽略掉头时间),其中甲车从A城开出,乙车从B城开出,两车在距A城24公里处第一次相遇.当甲车还没有到达B城时,两车又相遇一次,并且后来再在距B城12公里处第三次相遇.那么第二次相遇时,两车距离B城 公里.
考点:应用类问题
专题:
分析:可在一条线段上简单的作出图形,考虑两车第二次相遇的情形,即甲还没有到达B城,便与乙相遇于D处,其实是乙到达A城后,在回程途中追上甲,这样甲到达D,B之间的E处时,乙到达B城折回与甲第三次相遇,又其速度不变,所以设法求出其速度之间的关系求出即可.
解答:解:设两车首次相遇于C处,第二次相遇于D处,第三次相遇于E处,考虑两车第二次相遇的情形,如图1,
甲还没有到达B城,便与乙相遇于D处,其实是乙到达A城后,在回程途中追上甲,
这样甲到达D,B之间的E处时,乙到达B城折回与甲第三次相遇,
则两车首次相遇时合开的路程记为S=AB,
第一、三次相遇之间,甲开行距离为CE,乙开行距离为CA+AB+BE,两车合开的路程为2S,
由于速度不变,甲应开行了2×24=48公里,即CE=48公里,
而题设EB=12公里,
所以S=AC+CE+EB=24+48+12=84公里,BC=S-AC=84-24=60公里,甲、乙速度之比=24:60=2:5,
于是易算得两车第一次相遇于C后,乙到达A站时,甲到达F处,CF=9.6公里,如图2,

从而乙在回程图中追赶甲,需从A起,追赶24+9.6+33.6÷(5-2)=44.8公里,
即AD=44.8公里,从而知DB=S-AD=84-44.8=39.2(公里).
故答案为:39.2.
甲还没有到达B城,便与乙相遇于D处,其实是乙到达A城后,在回程途中追上甲,
这样甲到达D,B之间的E处时,乙到达B城折回与甲第三次相遇,
则两车首次相遇时合开的路程记为S=AB,
第一、三次相遇之间,甲开行距离为CE,乙开行距离为CA+AB+BE,两车合开的路程为2S,
由于速度不变,甲应开行了2×24=48公里,即CE=48公里,
而题设EB=12公里,
所以S=AC+CE+EB=24+48+12=84公里,BC=S-AC=84-24=60公里,甲、乙速度之比=24:60=2:5,
于是易算得两车第一次相遇于C后,乙到达A站时,甲到达F处,CF=9.6公里,如图2,

从而乙在回程图中追赶甲,需从A起,追赶24+9.6+33.6÷(5-2)=44.8公里,
即AD=44.8公里,从而知DB=S-AD=84-44.8=39.2(公里).
故答案为:39.2.
点评:本题主要考查了路程问题中的追及相遇问题,对于此类应用问题,能够通过作出一个简单的图形帮助理清思路,从而求解.

练习册系列答案
相关题目
下列各数中,是负数的是( )
| A、-(-2) |
| B、-(-3)2 |
| C、|-3| |
| D、-(-1)3 |
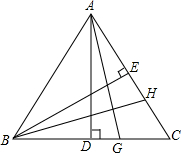 如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.
如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.