题目内容
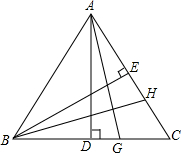
 如图,等边△ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD,求证:
如图,等边△ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD,求证:(1)∠CAE=∠BCD;
(2)AF=2FG.
考点:全等三角形的判定与性质,等边三角形的判定与性质,含30度角的直角三角形
专题:
分析:(1)易证BD=CE,即可证明△BCD≌△CAE,可得∠CAE=∠BCD,即可解题;
(2)易证∠CFE=∠ACE,即可求得∠AFG=60°,根据AG⊥CD,即可求得∠FAG=30°,即可解题.
(2)易证∠CFE=∠ACE,即可求得∠AFG=60°,根据AG⊥CD,即可求得∠FAG=30°,即可解题.
解答:证明:(1)∵△ABC是等边三角形,
∴AB=BC,
∵AD=BE,∴BD=CE,
在△BCD和△CAE中,
,
∴△BCD≌△CAE(SAS),
∴∠CAE=∠BCD;
(2)∵∠CAE+∠ACE+∠AEC=180°,∠BCD+∠AEC+∠CFE=180°,
∴∠CFE=∠ACE=60°,
∴∠AFG=60°,
∵AG⊥CD,∴∠FAG=30°,
∴AF=2FG.
∴AB=BC,
∵AD=BE,∴BD=CE,
在△BCD和△CAE中,
|
∴△BCD≌△CAE(SAS),
∴∠CAE=∠BCD;
(2)∵∠CAE+∠ACE+∠AEC=180°,∠BCD+∠AEC+∠CFE=180°,
∴∠CFE=∠ACE=60°,
∴∠AFG=60°,
∵AG⊥CD,∴∠FAG=30°,
∴AF=2FG.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△BCD≌△CAE是解题的关键.

练习册系列答案
相关题目
下列各数中,是负数的是( )
| A、-(-2) |
| B、-(-3)2 |
| C、|-3| |
| D、-(-1)3 |
已知正比例函数的图象经过点(1,2),(a,-2),则a的值为( )
| A、-1 | ||
| B、1 | ||
C、
| ||
D、-
|
 一次函数y=kx+b的图象如图所示,则该一次函数的表式( )
一次函数y=kx+b的图象如图所示,则该一次函数的表式( )A、y=-
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
 如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.
如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.
