题目内容
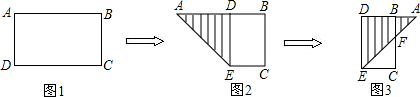
如图:有一张长方形纸片ABCD,AB=3,AD=1.8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC相交于点F,则CF的长为 .

考点:翻折变换(折叠问题)
专题:
分析:根据翻折的性质判断出△ADE是等腰直角三角形,然后求出AD=DE,再求出DB,然后求出BF,然后根据CF=BC-BF计算即可得解.
解答:解:∵将纸片折叠AD边落在AB边上,
∴∠A=
×90°=45°,
∴△ADE是等腰直角三角形,
∴AD=DE=1.8,
∵AB=3,
∴DB=AB-AD=3-1.8=1.2,
又∵∠ABF=90°,
∴∠ABF是等腰直角三角形,
∴BF=1.8-1.2=0.6,
∴CF=BC-BF=1.8-0.6=1.2.
故答案为:1.2.
∴∠A=
| 1 |
| 2 |
∴△ADE是等腰直角三角形,
∴AD=DE=1.8,
∵AB=3,
∴DB=AB-AD=3-1.8=1.2,
又∵∠ABF=90°,
∴∠ABF是等腰直角三角形,
∴BF=1.8-1.2=0.6,
∴CF=BC-BF=1.8-0.6=1.2.
故答案为:1.2.
点评:本题考查了翻折变换的性质,等腰直角三角形的判定与性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
 一次函数y=kx+b的图象如图所示,则该一次函数的表式( )
一次函数y=kx+b的图象如图所示,则该一次函数的表式( )A、y=-
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
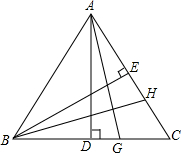 如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.
如图,等边△ABC中,AD、BE是高,G、H分别是BC、AC上的点,且AG=BH.求证:CG=CH.
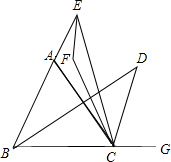 已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.
已知,E、G分别是BA、BC延长线上任意一点,∠ABC、∠ACG的平分线相交于点D,∠ACE、∠AEC的平分线相交于点F,请你猜想∠F与∠D的关系,并证明你的猜想.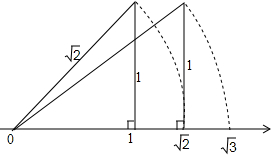 如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为
如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为