题目内容
20.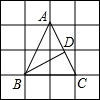 如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{4}{5}$ |
分析 利用勾股定理求得相关线段的长度,然后由面积法求得BD的长度,再利用勾股定理即可求出CD的长.
解答 解:如图,由勾股定理得 AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
∵$\frac{1}{2}$BC×2=$\frac{1}{2}$AC•BD,
即$\frac{1}{2}$×2×2=$\frac{1}{2}$×$\sqrt{5}$•BD,
∴BD=$\frac{4\sqrt{5}}{5}$,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\frac{2\sqrt{5}}{5}$,
故选:A.
点评 本题考查了勾股定理,三角形的面积.利用面积法求得线段BD的长度是解题的关键.

练习册系列答案
相关题目
 已知如图:△ABC中,∠ACB=90°
已知如图:△ABC中,∠ACB=90°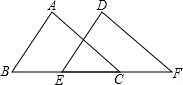 如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.
如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若根据“ASA”说明△ABC≌△DEF,则应添加条件∠ACB=DFE.或AC∥DF.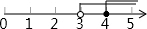



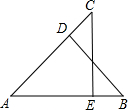 如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.
如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.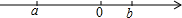 已知有理数a,b在数轴上的位置如图所示,那么
已知有理数a,b在数轴上的位置如图所示,那么