题目内容
9．解方程组$\left\{\begin{array}{l}{3x+2y=19}\\{2x-y=1}\end{array}\right.$．分析 方程组利用代入消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{3x+2y=19①}\\{2x-y=1②}\end{array}\right.$，
由②得：y=2x-1③，
把③代入①得：3x+2（2x-1）=19，即x=3，
把x=3代入③得：y=5，
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$．
点评 此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
（1）如图，已知点C在线段AB上，且AC=6cm，BC=4cm，点M、N分别是AC、BC的中点，求线段MN的长度；
20．
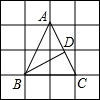如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为（ ）
如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{3\sqrt{5}}{5}$ | C． | $\frac{4\sqrt{5}}{5}$ | D． | $\frac{4}{5}$ |
把19个边长为2cm的正方体重叠起来，作成如图那样的立体图形，求这个立体图形的表面积．
4．如图（一），在边长为a的正方形中，挖掉一个边长为b的小正方形（a＞b），把余下的部分剪成一个矩形（如图（二）），通过计算两个图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
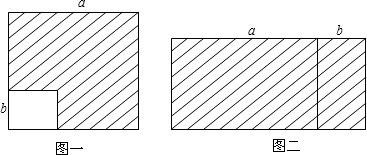
| A． | （a+b）2=a2+2ab+b2 | B． | a2-b2=（a+b）（a-b） | ||
| C． | （a-b）2=a2-2ab+b2 | D． | （a+2b）（a-b）=a2+ab-2b2 |
14．已知$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是关于x，y的方程组$\left\{\begin{array}{l}{ax-2y=5}\\{3x+by=-3}\end{array}\right.$的解，那么（ ）
| A． | a=$\frac{3}{2}$，b=9 | B． | a=$\frac{3}{2}$，b=-9 | C． | a=-9，b=0 | D． | a=6，b=3 |
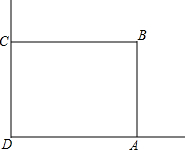在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角AD，DC（两强足够长）用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm，若围成的花园面积为192m2，求x的值．