题目内容
5.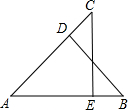 如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.
如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边AB与AC,AD与AE,BD与CE.
分析 根据全等三角形的对应角所对的边的对应边求解.
解答 解:∵△ABD≌△ACE,
∴AB=AC,AD=AE,BD=CE,
即AB与AC,AD与AE,BD与CE为对应边.
故答案为AB与AC,AD与AE,BD与CE.
点评 本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等,全等三角形的对应边上的高、中线以及对应角的平分线相等,全等三角形的周长相等,面积相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.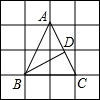 如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
 如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{4}{5}$ |
14.已知$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是关于x,y的方程组$\left\{\begin{array}{l}{ax-2y=5}\\{3x+by=-3}\end{array}\right.$的解,那么( )
| A. | a=$\frac{3}{2}$,b=9 | B. | a=$\frac{3}{2}$,b=-9 | C. | a=-9,b=0 | D. | a=6,b=3 |
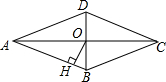 如图,菱形ABCD的对角线AC、BD相交于点O,∠ADC=135°,过点O作OH⊥AB,垂足为H,则∠AOH=67.5度.
如图,菱形ABCD的对角线AC、BD相交于点O,∠ADC=135°,过点O作OH⊥AB,垂足为H,则∠AOH=67.5度. 如图,∠1是Rt△ABC的一个外角,点D、E分别为边AB、AC的中点,∠1=110°,则∠2的度数是20°.
如图,∠1是Rt△ABC的一个外角,点D、E分别为边AB、AC的中点,∠1=110°,则∠2的度数是20°. 把19个边长为2cm的正方体重叠起来,作成如图那样的立体图形,求这个立体图形的表面积.
把19个边长为2cm的正方体重叠起来,作成如图那样的立体图形,求这个立体图形的表面积.