题目内容
3.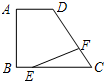 已知:如图,直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,$sinC=\frac{4}{5}$,若点E,F分别是BC,CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1个单位的速度同时出发,连接EF.求△EFC面积的最大值为10.
已知:如图,直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,$sinC=\frac{4}{5}$,若点E,F分别是BC,CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1个单位的速度同时出发,连接EF.求△EFC面积的最大值为10.
分析 本题要先求出三角形EFC的面积与时间的函数关系式,可根据E,F的速度用时间t表示出CE,CF的长,△CEF中,可以用CE作底边,以CF•sinC作高,可据此得出三角形CEF的面积和时间t的函数关系式,根据函数的性质即可求出EFC的面积最大值和对应的时间t的值,然后根据时间t确定出E、F的具体位置.
解答 解:设运动时间为x秒,则有BE=CF=x,EC=10-x,
如图,过点F作FN⊥BC,垂足为N,
在Rt△FNC中,FN=CF•sinC=$\frac{4}{5}$x,
∴S△EFC=$\frac{1}{2}$EC•FN=$\frac{1}{2}$(10-x)×$\frac{4}{5}$x=-$\frac{2}{5}{x}^{2}$+4x,
当x=-$\frac{4}{2×(-\frac{2}{5})}$=5时,S△EFC=-$\frac{2}{5}×{5}^{2}$+4×5=10,
即△EFC面积的最大值为10,
此时,点E,F分别在BC,CD的中点处.
故答案为:10.
点评 本题主要考查了梯形的性质、图形面积的求法以及二次函数的综合应用等知识点,解决本题的关键是二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
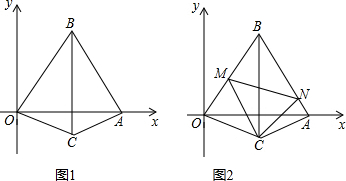
12. 如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
 如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减少 |
 如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.
如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.