题目内容

13．若最简二次根式$\sqrt{x+1}$与-2$\sqrt{2x}$能合并为一个二次根式，则x=1．

分析 根据最简二次根式能合并，可得同类二次根式，根据同类二次根式的被开方数相同，可得关于x的方程．

解答 解：由最简二次根式$\sqrt{x+1}$与-2$\sqrt{2x}$能合并为一个二次根式，得
x+1=2x．
解得x=1，
故答案为：1．

点评 本题考查了同类二次根式，利用同类二次根式得出方程是解题关键．

练习册系列答案
相关题目
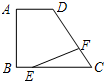3．已知：如图，直角梯形ABCD中，AD∥BC，∠A=90°，BC=CD=10，$sinC=\frac{4}{5}$，若点E，F分别是BC，CD上的动点，点E从点B出发向点C运动，点F从点C出发向点D运动，若两点均以每秒1个单位的速度同时出发，连接EF．求△EFC面积的最大值为10．
4．（1）求x的值：（2x-1）2-169=0．
（2）计算：（-1）2013+$\root{3}{27}$+|1-$\sqrt{2}$|-$\sqrt{2}$．
1．（1）（+12）+（-23）-（-33）
（2）（-1）10×2+（-2）3÷4+（-22）
（3）（$\frac{2}{3}$-$\frac{1}{4}$-$\frac{3}{8}$+$\frac{5}{24}$）×48       
（4）-（a-b）-3（b-2a）
8．下列各式中计算正确的是（　　）
A．$\sqrt{-4}$$\sqrt{-16}$=（-2）（-4）=8B．$\sqrt{8{a^2}}=4a（a＞0）$C．$\sqrt{{3^2}+{4^2}}=3+4=7$D．（$\sqrt{3}$+2）2=7+4$\sqrt{3}$
18．已知一个正数的平方根分别是3-a和2a+b，则这个正数是81．
5．先化简，再求值：$（{\frac{{{x^2}-2x+1}}{{{x^2}-1}}+\frac{1}{x}}）÷\frac{1}{x+1}$，其中x=2．
2．A、B两地之间的路程是36km，小丽从A地骑自行车到B地，小明从B地骑自行车到A地，两人同时出发，相向而行，经过1h后两人相遇；再过0.5h，小丽余下的路程是小明余下路程的2倍．小明和小丽骑车的速度各是多少？
3．下列计算正确的是（　　）
A．2a+3b=5abB．2a-2=$\frac{1}{2{a}^{2}}$C．a3•a2=a6D．（a2）4=a8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网