Question

3．函数y=$\frac{k}{x}$与y=m-x的图象的一个交点是A（2，3），其中k、m为常数．
（1）求k、m的值，画出函数的草图．
（2）根据图象，确定自变量x的取值范围，使一次函数的函数值大于反比例函数的函数值．

Answer 1

分析 （1）把点A的坐标代入函数解析式可得k，m，利用特殊点画出草图即可；
（2）先列方程组求另一个交点B的坐标，再根据图象交点可得结论．

解答 \解：（1）把x=2，y=3代入解析式得，k=xy=2×3=6，m=x+y=2+3=5，
则y=$\frac{6}{x}$，y=-x+5，
草图如下：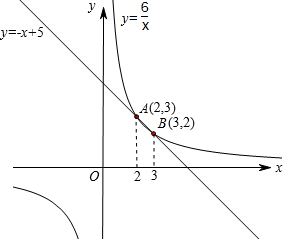

（2）由题意得：$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=-x+5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=3}\end{array}\right.$     $\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=2}\end{array}\right.$，
∴函数y=$\frac{6}{x}$与y=5-x的图象的另一个交点是B（3，2），
由图象得：当2＜x＜3或x＜0时，一次函数的函数值大于反比例函数的函数值．

点评 本题考查了反比例函数和一次函数的交点问题，还考查了利用特殊点画函数的图象；解决此类问题的一般步骤是：（1）求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点；（2）根据图象，确定自变量x的取值范围时，要根据图象得出．