Question

13．圆上任取三点所构成的三角形是钝角三角形是什么事件？若是随机事件，则构成钝角三角形的概率是多少？

Answer 1

分析 根据题意，将圆按逆时针方向依次标记三点为A、B、C，设出弧AB、弧AC、弧BC的长度，得到所有可能结果构成的平面区域与“三点组成锐角三角形”构成的平面区域，分别计算出两个区域的面积，再利用几何概型公式加以计算，可得构成锐角或直角三角形的概率，即可得出结论．

解答 解：圆上任取三点所构成的三角形是钝角三角形是随机事件，
如图1，设圆的半径为1，按逆时针方向依次表记三点为A、B、C，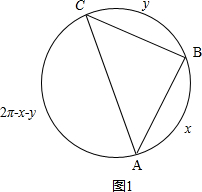

设弧AB=x，弧BC=y，弧AC=2π-x-y，
依题意，所有可能的结果构成的平面区域为：Ω={（x，y）|0＜x＜2π，0＜y＜2π，0＜2π-x-y＜2π}，
事件A=“三点组成锐角或直角三角形”，构成的平面区域为：A={（x，y）∈Ω|0＜x≤π，0＜y＜π，0＜2π-x-y＜π}，
分别作出Ω与A中不等式组对应的平面区域，得到两个三角形及其内部区域，如图2所示，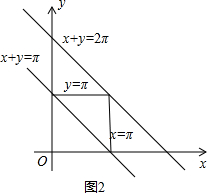

∵平面区域Ω的面积为2π²，平面区域A的面积为$\frac{1}{2}$×π×π=$\frac{1}{2}$π²，
∴所求概率为：P（A）=$\frac{1}{4}$，
∴圆上任取三点所构成的三角形是钝角三角形的概率为1-$\frac{1}{4}$=$\frac{3}{4}$．

点评 本题给出圆周上的任意三点，求此三点构成钝角三角形的概率，着重考察了圆内接三角形、二元一次不等式组表示的平面区域和几何概型计算公式．