题目内容
8.如果函数y=(a-1)x2+3x+$\frac{a+5}{a-1}$的图象经过平面直角坐标系的四个象限,求a的取值范围.分析 函数图象经过四个象限,需满足3个条件:
(Ⅰ)函数是二次函数;
(Ⅱ)二次函数与x轴有两个交点;
(Ⅲ)两个交点必须要在y轴的两侧,即两个交点异号.
解答 解:函数图象经过四个象限,需满足3个条件:
(I)函数是二次函数.因此a-1≠0,即a≠1①;
(II)二次函数与x轴有两个交点.因此△=9-4(a-1)$\frac{a+5}{a-1}$=-4a-11>0,解得a<-$\frac{11}{4}$②;
(III)两个交点必须要在y轴的两侧.因此$\frac{a+5}{(a-1)^{2}}$<0,解得a<-5③;
综合①②③式,可得:a<-5.
点评 本题考查二次函数的图象与性质、二次函数与x轴的交点、二次函数与y轴交点等知识点,解题关键是确定“函数图象经过四个象限”所满足的条件.

练习册系列答案
相关题目
19.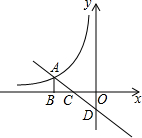 如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
 如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )| A. | $-\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (-a3)2=a6 | C. | 2a+3a2=5a3 | D. | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
20. 通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
 通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )| A. | (a-b)2=a2-2ab+b2 | B. | 2a(a+b)=2a2+2ab | C. | (a+b)2=a2+2ab+b2 | D. | (a+b)(a-b)=a2-b2 |
17.下列四个实数中,绝对值最大的数是( )
| A. | -$\sqrt{20}$ | B. | $\sqrt{15}$ | C. | $\root{3}{19}$ | D. | -$\root{3}{62}$ |
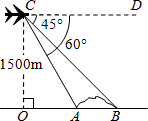 如图,在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求油污带AB的长.(参考数据:$\sqrt{3}$=1.73)
如图,在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求油污带AB的长.(参考数据:$\sqrt{3}$=1.73)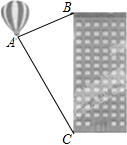 如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.
如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.