题目内容
Rt△ABC中，∠C=90°，AB=2，则AB2+BC2+CA2= ．
考点：勾股定理
专题：
分析：由△ABC为直角三角形，利用勾股定理得到斜边的平方等于两直角边的平方和，根据斜边AB的长，可得出两直角边的平方和，然后将所求式子的后两项结合，将各自的值代入即可求出值．
解答：
解：∵Rt△ABC中，∠C=90°，
∴AB是斜边，
∴CA2+BC2=AB2，
又∵AB=2，
∴CA2+BC2=AB2=4，
则AB2+BC2+CA2=AB2+（BC2+CA2）=4+4=8．
故答案为：8．
解：∵Rt△ABC中，∠C=90°，∴AB是斜边，
∴CA2+BC2=AB2，
又∵AB=2，
∴CA2+BC2=AB2=4，
则AB2+BC2+CA2=AB2+（BC2+CA2）=4+4=8．
故答案为：8．
点评：本题考查了勾股定理，整体解答AC2+BC2是解题的关键．
练习册系列答案
相关题目
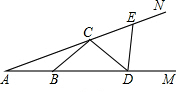如图，点B、D在射线AM上，点C、E在射线AN上，且AB=BC=CD=DE，已知∠DEN=105°，则∠A的度数是
如图，矩形ABCD中，AD=10，AB=8，点P在边CD上，且BP=BC，点M在线段BP上，点N在线段BC的延长线上，且PM=CN，连接MN交CP于点F，过点M作ME⊥CP于E，则EF=
按图填空，如图：