题目内容
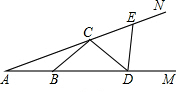如图，点B、D在射线AM上，点C、E在射线AN上，且AB=BC=CD=DE，已知∠DEN=105°，则∠A的度数是考点：等腰三角形的性质
专题：
分析：根据邻补角的定义可得∠AED的度数，再根据等边对等角和三角形内角和定理可得∠CDE的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和以及等腰三角形的性质可得∠A+∠ADC=3∠A，再根据∠DEN=∠CDE+3∠A，列出方程计算即可求解．
解答：解：∵∠DEN=105°，
∴∠AED=75°，
∵CD=DE，
∴∠ECD=∠AED=75°，
∴∠CDE=30°，
∵AB=BC，
∴∠A=∠ACB，
∴∠CBD=2∠A，
∵BC=CD，
∴∠CDB=∠CBD=2∠A，
∴∠DEN=∠CDE+3∠A，即105°=30°+3∠A，
解得∠A=25°．
故答案为：25°．
∴∠AED=75°，
∵CD=DE，
∴∠ECD=∠AED=75°，
∴∠CDE=30°，
∵AB=BC，
∴∠A=∠ACB，
∴∠CBD=2∠A，
∵BC=CD，
∴∠CDB=∠CBD=2∠A，
∴∠DEN=∠CDE+3∠A，即105°=30°+3∠A，
解得∠A=25°．
故答案为：25°．
点评：本题考查了等腰三角形两底角相等的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及邻补角的定义．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，小明从点A处出发，沿着坡角为α的斜坡向上走了0.65千米到达点B，sinα=