题目内容
14.商场某种商品平均每天可销售40件,每件盈利60元.为减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多销售2件.(1)每件商品降价多少元时,商场日盈利可达到3150元?
(2)商场日盈利能否达到3300元?
(3)每件商品降价多少元时,商场日盈利最多?
分析 (1)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数40+2×降价的钱数),把相关数值代入求解即可;
(2)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数40+2×降价的钱数),整理后判断方程的根的情况即可;
(3)根据(1)得到的关系式判断出二次函数的对称轴,此时二次函数取到最值.
解答 解:(1)设降价x元,由题意得:(60-x)(40+2x)=3150,
化简得:x2-40x+375=0,
解得:x1=15,x2=25,
答:每件商品降价25元或15元,商场日盈利可达3150元;
(2)设降价x元,由题意得:(60-x)(40+2x)=3300,
化简得:x2-40x+450=0,
b2-4ac=1600-4×450=-200<0,
故此方程无实数根,
故商场日盈利不能达到3300元;
(3)设利润为y元,根据题意可得:
y=(60-x)(40+2x)
=-2x2+80x+2400
=-2(x2-40x)+2400
=-2(x-20)2+3200
故当x=20时,y最大.
答:每件商品降价20元时,商场日盈利的最多.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用;得到日盈利的等量关系是解决本题的关键.

练习册系列答案
相关题目
19. 如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )
如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )
 如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )
如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )| A. | 100 | B. | 120 | C. | 130 | D. | 140 |
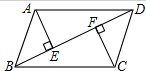 如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.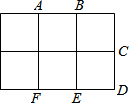 如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10.
如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10. 铭铭用两个大小不一的正方体木块组成了一个几何体,该几何体的主视图如图所示,则该几何体的俯视图为( )
铭铭用两个大小不一的正方体木块组成了一个几何体,该几何体的主视图如图所示,则该几何体的俯视图为( )



 如图,△ABC中,∠ACB=90°,CD是中线,求证:AB=2CD.
如图,△ABC中,∠ACB=90°,CD是中线,求证:AB=2CD.