题目内容
19. 如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )
如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )| A. | 100 | B. | 120 | C. | 130 | D. | 140 |
分析 由AB切圆O1于B点,AC切圆O2于C点,得到∠ABO1=∠ACO2=90°,由等腰三角形的性质得到∴∠O1BD=70°,∠O2CE=60°,根据三角形的内角和求得.
解答 解:∵AB切圆O1于B点,AC切圆O2于C点,
∴∠ABO1=∠ACO2=90°,
∵O1D=O1B,O2E=O2C,
∴∠O1BD=∠O1DB=$\frac{180°-40°}{2}$=70°,∠O2CE=∠O2EC=$\frac{1}{2}$(180°-60°)=60°,
∴∠ABC=20°,∠ACB=30°,
∴∠A=130°,
故选C.
点评 本题考查了切线的性质,等腰三角形的性质,三角形的内角和定理,熟记定理是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.已知空气的单位体积质量为0.00124克/厘米3,将0.00124这个数用科学记数法表示为( )
| A. | 0.124×10-2 | B. | 1.24×10-3 | C. | 1.24×103 | D. | 1.24×102 |
 如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长.
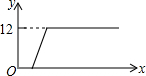
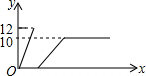
如图,已知点C为AB上一点,AC=12cm,CB=$\frac{1}{2}$AC,D、E分别为AC、AB的中点,求DE的长.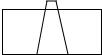 如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )
如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是( )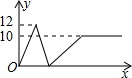
 如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.
如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.