题目内容
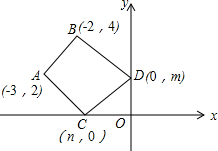 如图,A(-3,2),B(-2,4),C(n,0),D(0,m),若四边形ABCD的周长最小,求-
如图,A(-3,2),B(-2,4),C(n,0),D(0,m),若四边形ABCD的周长最小,求-| m |
| n |
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:过点B作关于y轴的对称点B′,过点A作关于x轴的对称点A′,连接A′B′分别交x、y轴于点D、C,由两点之间线段最短可知线段A′B′即为四边形ABCD的周长最小值,用待定系数法求出过A′B′两点的直线解析式,即可求出C、D的坐标.
解答: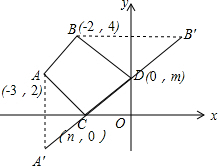 解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,
解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,
∴求其周长最小值,就是求BD+CD+AC的最小值.
过B作y轴对称点B′(2,4),
则BD=B′D,
过A作x轴对称点A′(-3,-2),则AC=A′C,
∴BC+CD+AD=B′C+CD+A′D=A′B′,
此时四边形的周长最小;
设直线A′B′的方程是y=kx+b(k≠0),
∴
,解得
,
故过A′B′两点的一次函数解析式为y=
x+
,
∴C(-
,0)D(-0,
),
即n=-
,m=
,
∴-
=-
=
.
 解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,
解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,∴求其周长最小值,就是求BD+CD+AC的最小值.
过B作y轴对称点B′(2,4),
则BD=B′D,
过A作x轴对称点A′(-3,-2),则AC=A′C,
∴BC+CD+AD=B′C+CD+A′D=A′B′,
此时四边形的周长最小;
设直线A′B′的方程是y=kx+b(k≠0),
∴
|
|
故过A′B′两点的一次函数解析式为y=
| 6 |
| 5 |
| 8 |
| 5 |
∴C(-
| 4 |
| 3 |
| 8 |
| 5 |
即n=-
| 4 |
| 3 |
| 8 |
| 5 |
∴-
| m |
| n |
| ||
-
|
| 6 |
| 5 |
点评:本题考查的是两点之间线段最短及用待定系数法求一次函数的解析式,根据对称的性质作出A、B的对称点A′、B′及求出其坐标是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列几组数:①9,12,15;②15,36,39;③12,35,35;④12,18,22.其中能组成直角三角形边长的是( )
| A、①和② | B、②和③ |
| C、③和④ | D、①和④ |
如果|
|=3.|
|=2,且
与
反向,那么下列关系中成立的是( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
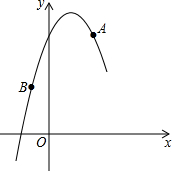 如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )| A、(-2,0) |
| B、(0.5,6.5) |
| C、(3,2) |
| D、(2,2) |
 如图,如果∠1=∠2=∠3,则AM为△
如图,如果∠1=∠2=∠3,则AM为△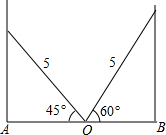 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.
如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长. 如图,在正方形ABCD中,F是DC边的中点,E为BC边上的一点,且EC=
如图,在正方形ABCD中,F是DC边的中点,E为BC边上的一点,且EC= 如图,时钟的钟面上标有1,2,3…,12共12个数,一条直线把钟面分成了两部分.请你再画一条直线分割钟面,使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等.
如图,时钟的钟面上标有1,2,3…,12共12个数,一条直线把钟面分成了两部分.请你再画一条直线分割钟面,使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等.