Question

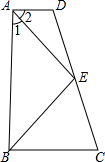如图，AD∥BC，∠1=∠2，E是DC的中点．
（1）量得：图1中AD≈

 

cm，BC≈

 

cm，AB≈

 

cm；
（2）猜想：AD、BC、AB之间的数量关系为

 

，请你对你的猜想加以证明．

Answer 1

考点：全等三角形的判定与性质,勾股定理

专题：

分析：在AB上找到一点F，使得AF=AD，易证△ADE≌△AFE，可得∠AFE=∠D，DE=EF，即可求得CE=EF，∠BFE=∠C，根据余弦定理可求得BC=BF，即可解题．

解答：解：在AB上找到一点F，使得AF=AD，

∵在△ADE和△AFE中，

AD=AF ∠1=∠2 AE=AE

，
∴△ADE≌△AFE，（SAS）
∴∠AFE=∠D，DE=EF，
∵D是CD中点，∴CE=DE，
∴CE=EF，
∴∠D+∠C=180°，∠AFE+∠BFE=180°，
∴∠BFE=∠C，
∵BE²=CE²+BC²-2BC•CE•cos∠C，
BE²=EF²+BF²-2EF•BF•cos∠BFE，BE是公共边，
∴BF=BC，
∵AB=AF+BF，
∴AB=AD+BC．
故答案为 1.5，2.5，4，AB=AD+BC．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边、对应角相等的性质，本题中求证△ADE≌△AFE是解题的关键．