题目内容
在梯形ABCD中,AD∥BC,AB⊥BC,垂足为B,AB=2,DC切以AB为直径的⊙O于点E,设AD=a,BC=b,求ab的值.
考点:切线的性质
专题:
分析:过D作DF⊥BC于点F,则DF=AB=2,CF=b-a.根据切线长定理可得DE=AD=a,EC=BC=b,则CD=a+b,在直角△CDF中利用勾股定理即可求解.
解答: 解:过D作DF⊥BC于点F,则DF=AB=2,CF=b-a.
解:过D作DF⊥BC于点F,则DF=AB=2,CF=b-a.
∵AD、BC和CD是圆的切线,
∴DE=AD=a,EC=BC=b,
∴CD=a+b,
∵在直角△CDF中,DF2+FC2=CD2,
∴22+(b-a)2=(a+b)2,
解得:ab=1.
 解:过D作DF⊥BC于点F,则DF=AB=2,CF=b-a.
解:过D作DF⊥BC于点F,则DF=AB=2,CF=b-a.∵AD、BC和CD是圆的切线,
∴DE=AD=a,EC=BC=b,
∴CD=a+b,
∵在直角△CDF中,DF2+FC2=CD2,
∴22+(b-a)2=(a+b)2,
解得:ab=1.
点评:本题考查了切线长定理和勾股定理,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、所有的有理数都可以在数轴上表示出来 |
| B、在数轴上0和-1之间没有负数 |
| C、数轴上在原点两旁到原点的距离相等的点表示的数互为相反数 |
| D、数轴上表示-3的点与表示+1的点距离是4个单位长度 |
 如图,一张直角三角形纸片,两直角边AC=6cm,BC=8cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后部分△ADE的面积.
如图,一张直角三角形纸片,两直角边AC=6cm,BC=8cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后部分△ADE的面积.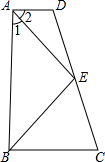 如图,AD∥BC,∠1=∠2,E是DC的中点.
如图,AD∥BC,∠1=∠2,E是DC的中点. 如图,在△ABC中,AB=5,BC=7,AC=4
如图,在△ABC中,AB=5,BC=7,AC=4