题目内容
14．（-2）2+（-2）-2=$\frac{17}{4}$．分析 根据乘方的意义和负指数的意义解答即可．
解答 解：原式=$4+\frac{1}{4}=\frac{17}{4}$，
故答案为：$\frac{17}{4}$．
点评 本题主要考查的是负指数的意义：负指数具有倒数的意义，即${a}^{-n}=\frac{1}{{a}^{n}}$（a≠0）．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
4．某校九年级在母亲节倡议“感恩母亲，做点家务”活动．为了解同学们在母亲节的周末做家务情况，年级随机调查了部分同学，并用得到的数据制成如下不完整的统计表．
（1）统计表中的x=80，y=200；
（2）被调查同学做家务时间的中位数是1.5小时，平均数是1.32小时；
（3）年级要组织一次“感恩母亲“的主题级会，级长想从报名的4位同学中随机抽取2位同学在会上谈体会．据统计，报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人．请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率．
| 做家务时间 | 频数（人数） | 频率 |
| 0.5 | 24 | 0.12 |
| 1 | 60 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 36 | 0.18 |
| 合计 | y | 1 |
（2）被调查同学做家务时间的中位数是1.5小时，平均数是1.32小时；
（3）年级要组织一次“感恩母亲“的主题级会，级长想从报名的4位同学中随机抽取2位同学在会上谈体会．据统计，报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人．请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率．
如图，矩形ABCD中，点E，F分别在AB，CD边上，连接CE、AF，∠DCE=∠BAF．试判断四边形AECF的形状并加以证明．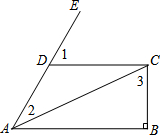
如图，CD∥AB，CB⊥AB，∠1=60°，∠2=40°，则∠3=70°．
作图题（作图工具不限，保留作图痕迹，写出结论）