题目内容
4.某校九年级在母亲节倡议“感恩母亲,做点家务”活动.为了解同学们在母亲节的周末做家务情况,年级随机调查了部分同学,并用得到的数据制成如下不完整的统计表.| 做家务时间 | 频数(人数) | 频率 |
| 0.5 | 24 | 0.12 |
| 1 | 60 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 36 | 0.18 |
| 合计 | y | 1 |
(2)被调查同学做家务时间的中位数是1.5小时,平均数是1.32小时;
(3)年级要组织一次“感恩母亲“的主题级会,级长想从报名的4位同学中随机抽取2位同学在会上谈体会.据统计,报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人.请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率.
分析 (1)由表格可求得总人数:y=60÷0.3=200,继而求得:x=200×0.4=80;
(2)由表格可得被调查同学做家务时间的中位数是:1.5小时;平均数是:$\frac{24×0.5+60×1+80×1.5+36×2}{200}$;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的情况,再利用概率公式即可求得答案.
解答 解:(1)∵总人数:y=60÷0.3=200,
∴x=200×0.4=80,
故答案为:80,200;
(2)被调查同学做家务时间的中位数是:1.5小时;
平均数是:$\frac{24×0.5+60×1+80×1.5+36×2}{200}$=1.32(小时);
故答案为:1.5;1.32;
(3)分别用A,B,C,D表示做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人;
画树状图得:
∵共有12种等可能的结果,选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的有4种情况,
∴P(恰好是一位做家务2小时和一位做家务1.5小时)=$\frac{4}{12}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.为了实现道路畅通工程,我省今年计划公路建设累计投资92.7亿元,该数据用科学记数法可表示为( )
| A. | 9.27×109 | B. | 92.7×108 | C. | 9.27×1010 | D. | 0.927×1010 |
16.设a=$\sqrt{17}$-1,a在两个相邻整数之间,则这两个整数是( )
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
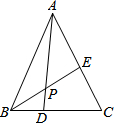 如图,在△ABC中,BD:DC=1:2,E是AC的中点,AD与BE相交于点P,P恰为BE中点,则AP:PD=3:1.
如图,在△ABC中,BD:DC=1:2,E是AC的中点,AD与BE相交于点P,P恰为BE中点,则AP:PD=3:1. 如图,在△ABC中,∠A=30°,∠B=45°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠A=30°,∠B=45°,BC=$\sqrt{6}$,求AB的长.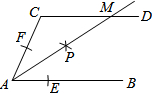 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为33°.
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为33°. 已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线.
已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线.