题目内容
 在直角坐标系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为
在直角坐标系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为考点:全等三角形的判定,坐标与图形性质
专题:分类讨论
分析:先求出BC的长,根据题意得出两种情况,画出图形,即可得出答案.
解答: 解:∵A(-1,0)、B(3,0)、C(0,2),
解:∵A(-1,0)、B(3,0)、C(0,2),
∴BC=
,
∴符合条件的有两种情况:①AD=BC=
,如图:
②BD=BC=
,如图:
即符合条件的D点坐标是(0,-2),(-2,-2),(2,2),
故答案为:(0,-2),(2,-2),(2,2).
 解:∵A(-1,0)、B(3,0)、C(0,2),
解:∵A(-1,0)、B(3,0)、C(0,2),∴BC=
| 13 |
∴符合条件的有两种情况:①AD=BC=
| 13 |
②BD=BC=
| 13 |
即符合条件的D点坐标是(0,-2),(-2,-2),(2,2),
故答案为:(0,-2),(2,-2),(2,2).
点评:本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知点A的坐标为(1,4),则点A关于y轴对称的点的横坐标为( )
| A、1 | B、-1 | C、4 | D、-4 |
若一个正n边形的一个外角为45°,则n等于( )
| A、6 | B、8 | C、10 | D、12 |
在以下四个图案中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 将正整数按如图所示的规律排列,若用有序数对(a,b)表示第a排,从左至右第b个数.
将正整数按如图所示的规律排列,若用有序数对(a,b)表示第a排,从左至右第b个数. 小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有
小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有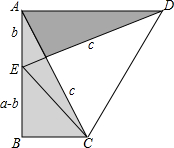 如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理.
如图,两个全等的直角△ABC和△DAE,两直角边的长分别为a,b,斜边长为c,使用两种不同的方法表示梯形ABCD的面积,并以此来验证勾股定理.