题目内容
13.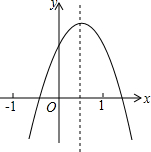 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a-b+c<0 |
分析 由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号,由x=-1时y的符号可确定a-b+c的符号.
解答 解:由抛物线的开口向下可得a<0,故A错误;
由抛物线的对称轴在y轴的右侧可得-$\frac{b}{2a}$>0.
∵a<0,∴b>0,故B错误;
由抛物线与y轴交点在y轴的正半轴可得c>0,故C错误;
由图可知当x=-1时,y=a-b+c<0,故D正确.
故选D.
点评 本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置,a-b+c的符号取决于x=-1时y的符号.

练习册系列答案
相关题目
5. 如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
 如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )| A. | 1个 | B. | 4个 | C. | 6个 | D. | 14个 |
3.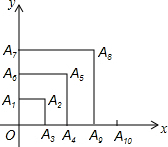 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )| A. | (0,672) | B. | (671,671) | C. | (672,672) | D. | (672,0) |
 如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.
如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.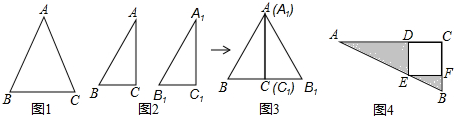
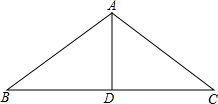 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.