题目内容
15.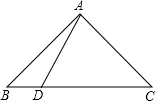 在△ABC中,已知AB=AC=10,BC=16,点D在BC上,且BD=$\frac{7}{2}$,连接AD,求证:AD⊥AC.
在△ABC中,已知AB=AC=10,BC=16,点D在BC上,且BD=$\frac{7}{2}$,连接AD,求证:AD⊥AC.
分析 过点A作AE⊥BC于E,由等腰三角形的性质得出BE=$\frac{1}{2}$BC=8,由勾股定理得:AE=6,AD2=AE2+DE2=$\frac{225}{4}$,DC2=(BC-BD)2=$\frac{625}{4}$,AC2=100,得出AC2+AD2=DC2,证出△DAC为直角三角形即可.
解答 证明:过点A作AE⊥BC于E,如图所示: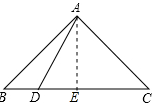
∵AB=AC=10,BC=16,
∴BE=$\frac{1}{2}$BC=8,
在Rt△ABE中,由勾股定理得:AE=6,
在Rt△ADE中,由勾股定理得:AD2=AE2+DE2=$\frac{225}{4}$,
在△ADC中:DC2=(BC-BD)2=$\frac{625}{4}$,AC2=100,
∴AC2+AD2=DC2,
∴△DAC为直角三角形,
∴DA⊥AC.
点评 本题考查了等腰三角形的性质、勾股定理、勾股定理的逆定理;熟练掌握等腰三角形的性质和勾股定理是解决问题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.已知关于x的方程2x+a-9=0的解是x=3,则a的值为( )
| A. | -7 | B. | 7 | C. | 3 | D. | -3 |
20.在2016年11月3日举行的第九届中国四部投资说明会上,现场签约116个项目,投资金额达130 944 000 000元,将130 944 000 000用科学记数法表示为( )
| A. | 1.30944×1012 | B. | 1.30944×1011 | C. | 1.30944×1010 | D. | 1.30944×109 |
 如图,点B,O,D在同一条直线上,若OA的方向是北偏东70°,则OD的方向是南偏东40°.
如图,点B,O,D在同一条直线上,若OA的方向是北偏东70°,则OD的方向是南偏东40°.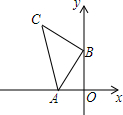 如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,3),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC,则点C的坐标是(-3.5).
如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,3),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC,则点C的坐标是(-3.5). 如图,将三角尺的直角顶点放在直尺的一边上,使∠1=60°,∠2=100°,则∠3=40°.
如图,将三角尺的直角顶点放在直尺的一边上,使∠1=60°,∠2=100°,则∠3=40°.