题目内容
14.(1)解方程:$\frac{1}{x-3}=2+\frac{x}{3-x}$(2)分解因式:a2(a-b)+b2(b-a)
分析 (1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,据此求解即可.
(2)应用提公因式法,分解因式a2(a-b)+b2(b-a)即可.
解答 解:(1)方程两边同乘以x-3,得:1=2(x-3)-x,
去括号,得:1=2x-6-x,
移项,合并同类项,得:x=7,
经检验x=7是原方程的解.
(2)a2(a-b)+b2(b-a)
=a2(a-b)-b2(a-b)
=(a2-b2)(a-b)
=(a+b)(a-b)(a-b)
=(a+b)(a-b)2
点评 此题主要考查了解分式方程的方法,以及分解因式的方法,要熟练掌握,解答此题的关键是要明确解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
相关题目
4. 一次函数y=kx-4的图象如图所示,则k的取值范围是( )
一次函数y=kx-4的图象如图所示,则k的取值范围是( )
 一次函数y=kx-4的图象如图所示,则k的取值范围是( )
一次函数y=kx-4的图象如图所示,则k的取值范围是( )| A. | k>1 | B. | k>0 | C. | k<0 | D. | k=0 |
9.代数式-4xy2+xy+1是( )
| A. | 二次二项式 | B. | 二次三项式 | C. | 三次二项式 | D. | 三次三项式 |
19.一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40min到达目的地,求前一小时的行驶速度.设原计划行驶的速度为xkm/h.
(1)根据题意填写下表(要求:填上适当的代数式,完成表格)
(2)列出方程(组),并求出问题的解.
(1)根据题意填写下表(要求:填上适当的代数式,完成表格)
| 速度(km/h) | 所走的路程(km) | 所用时间(h) | |
| 出发后第一小时内行驶 | x | x | 1 |
| 出发一小时以后行驶 | 1.5x | 180-x | $\frac{180-x}{1.5x}$ |
| 原计划行驶 | x | 180 | $\frac{180}{x}$ |
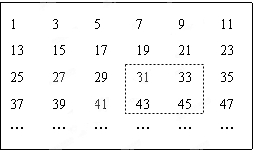 将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数.
将连续的奇数1,3,5,7,9…排成如图所示的数表,用长方形框选其中的四个数. 如图,点B,O,D在同一条直线上,若OA的方向是北偏东70°,则OD的方向是南偏东40°.
如图,点B,O,D在同一条直线上,若OA的方向是北偏东70°,则OD的方向是南偏东40°.