题目内容
1.边长为a的正三角形的内切圆的半径为( )| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{3}}{3}$a | D. | $\frac{\sqrt{3}}{6}$a |
分析 根据等边三角形的三线合一,可以构造一个由其内切圆的半径、外接圆的半径和半边组成的30°的直角三角形,利用锐角三角函数关系求出内切圆半径即可.
解答 解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
则∠OBD=30°,BD=$\frac{a}{2}$,
∴tan∠BOD=$\frac{OD}{BD}$=$\frac{\sqrt{3}}{3}$,
∴内切圆半径OD=$\frac{\sqrt{3}}{3}$×$\frac{a}{2}$=$\frac{\sqrt{3}}{6}$a.
故选D.
点评 此题主要考查了三角形的内切圆,注意:根据等边三角形的三线合一,可以发现其内切圆的半径、外接圆的半径和半边正好组成了一个30°的直角三角形.

练习册系列答案
相关题目
11.下列各式中,正确的是( )
| A. | a3+a2=a5 | B. | 2a+3b=5ab | C. | 7ab-3ab=4 | D. | x2y-2x2y=-x2y |
9.代数式-4xy2+xy+1是( )
| A. | 二次二项式 | B. | 二次三项式 | C. | 三次二项式 | D. | 三次三项式 |
13.无论k为何实数,二次函数y=x2-(3-k)x+k的图象总是过定点( )
| A. | (-1,4) | B. | (1,0) | C. | (1,4) | D. | (-1,0) |
10.已知关于x的方程2x+a-9=0的解是x=3,则a的值为( )
| A. | -7 | B. | 7 | C. | 3 | D. | -3 |
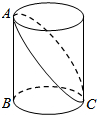 如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.
如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.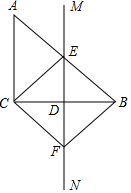 如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF.
如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF.