题目内容
3．
如图，在△ABC中，∠CAB=90°，DE、DF是△ABC的中位线，连接EF、AD，求证：EF=AD．
分析 由DE、DF是△ABC的中位线，根据三角形中位线的性质，即可求得四边形AEDF是平行四边形，又∠BAC=90°，则可证得平行四边形AEDF是矩形，根据矩形的对角线相等即可得EF=AD．
解答 证明：∵DE，DF是△ABC的中位线，
∴DE∥AB，DF∥AC，
∴四边形AEDF是平行四边形，
又∵∠BAC=90°，
∴平行四边形AEDF是矩形，
∴EF=AD．
点评 此题考查了三角形中位线的性质，平行四边形的判定与矩形的判定与性质．此题综合性较强，但难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
13．
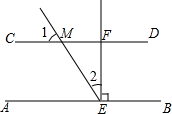如图，AB∥CD，EF⊥AB与E，EF交CD于F，FM交CD于M，已知∠1=55°，则∠MEB等于（ ）
如图，AB∥CD，EF⊥AB与E，EF交CD于F，FM交CD于M，已知∠1=55°，则∠MEB等于（ ）| A． | 120° | B． | 125° | C． | 130° | D． | 135° |
11．已知a，b，c为有理数，且a＜b，则下列不等式中正确的是（ ）
| A． | $\frac{a}{c}$＜$\frac{b}{c}$ | B． | ac＜bc | C． | a-c＞b-c | D． | a+c＜b+c |
18．若y=kx+2的函数值y随着x的增大而增大，则k的值可能是（ ）
| A． | 0 | B． | 1 | C． | -30 | D． | -2 |
8．
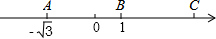如图，在数轴上，点A与点C到点B的距离相等，A，B两点所对应的实数分别是-$\sqrt{3}$和1，则点C对应的实数是（ ）
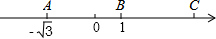如图，在数轴上，点A与点C到点B的距离相等，A，B两点所对应的实数分别是-$\sqrt{3}$和1，则点C对应的实数是（ ）| A． | 1+$\sqrt{3}$ | B． | 2+$\sqrt{3}$ | C． | 2$\sqrt{3}$-1 | D． | 2$\sqrt{3}$+1 |
如图，△ABC中，AB=AC=6，BC=4，∠A=40°．