题目内容
4.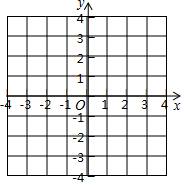 在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1
在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1>y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当-1<p<2时,点M关于y轴的对称点形成的图象与直线y=kx-4(k≠0)有交点,求k的取值范围.
分析 (1)将原抛物线的解析式配方化为顶点式,根据对称轴x=1列式可得m的值;
(2)把点E的横坐标代入y=-x2+2x求得E的坐标,根据对称轴得到其对称点,再由图形写出n的取值;
(3)先确定M的对称点的取值,及原抛物线关于y轴对称的抛物线,即可以看作是沿y轴翻折所得,计算两个边界点时直线y=kx-4的k值,写出结论即可.
解答 解:(1)∵y=-x2+2mx-m2-3+4m=-(x-m)2+4m-3,
对称轴是对称轴是直线x=1,
∴m=1,
∴抛物线的表达式为:y=-x2+2x;
(2)如图1:
当x=3时,y=-x2+2x=-9+6=-3,
∵抛物线的对称轴为x=1,
则E(3,y2)关于x=1对称点的坐标为(-1,-3),
由图象可知,-1<n<3时,y1>y2;
(3)由题意可得M′(-p,q),翻折后的函数表达式为y=-x2-2x,
∴结合-1<p<2,确定动点M及M′,
当x=-1时,y=-3;当x=2时,y=0,
因为动点M与M’关于y轴对称,所以图象确定如下,如图2,
当过(1,-3)时,代入 y=kx-4,k=1,
当过(-2,0)时,代入 y=kx-4,k=-2,
综上所述:k>1或k<-2.
点评 本题考查了利用条件确定二次函数的解析式、一次函数图象与系数k的关系、关于坐标轴对称的点的特点,运用了数形结合的思想,第三问的关键是理解“点M关于y轴的对称点形成的图象”,正确画出符合条件的图象,此题有难度,尤其是第三问.

练习册系列答案
相关题目
14.四个内角都相等的四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
13.某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
 如图,在菱形ABCD中,AB=5,对角线BD=6,DF⊥AB于点F.求DF的长.
如图,在菱形ABCD中,AB=5,对角线BD=6,DF⊥AB于点F.求DF的长.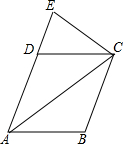 如图,点E是菱形ABCD的边AD延长线上的点,AE=AC,CE=CB,则∠B的度数为108°.
如图,点E是菱形ABCD的边AD延长线上的点,AE=AC,CE=CB,则∠B的度数为108°.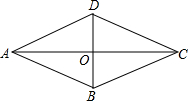 已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.
已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.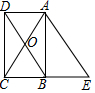 如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.
如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.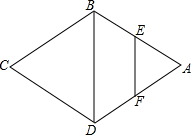 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.