题目内容
12.将方程5x2-6x+k=0化为(x+a)2=b的形式,并指出k为何值时方程有实数解?分析 先把常数项移项、化二次项系数为1,然后在等式的两边同时加上一次项系数-$\frac{6}{5}$的一半的平方,进行配方;根据根的判别式进行解答.
解答 解:5x2-6x+k=0,
x2-$\frac{6}{5}$x=-$\frac{k}{5}$,
x2-$\frac{6}{5}$x+$\frac{9}{25}$=-$\frac{k}{5}$+$\frac{9}{25}$,
(x-$\frac{3}{5}$)2=-$\frac{k}{5}$+$\frac{9}{25}$,
依题意得:△=36-20k≥0,
∴k≤$\frac{9}{5}$.
综上所述,k的取值范围是k≤$\frac{9}{5}$.
点评 本题考查了配方法解一元二次方程.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
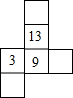 如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2-ab-ac-bc的值为76.
如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2-ab-ac-bc的值为76.