题目内容
13.若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是$\frac{{\sqrt{2}}}{2}$的概率为( )| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
分析 先根据特殊角的三角函数值填表,再根据概率公式求解即可.
解答 解:填表如下:
| α | 30° | 45° | 60° |
| sinα | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ |
| cosα | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ |
| tanα | $\frac{\sqrt{3}}{3}$ | 1 | $\sqrt{3}$ |
∴从表中任意取一个值,是$\frac{{\sqrt{2}}}{2}$的概率为$\frac{2}{9}$;
故选D.
点评 此题考查了概率公式,用到的知识点是特殊角的三角函数值和概率=所求情况数与总情况数之比;熟练掌握特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
3.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下面四个几何体中,主视图与其它几何体的主视图不同的是( )
| A. |  | B. |  | C. |  | D. |  |
18. 如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
 如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )| A. | $\frac{1}{2}$π | B. | $\frac{1}{2}π$+1 | C. | π | D. | π+1 |
2.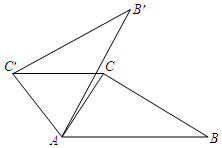 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
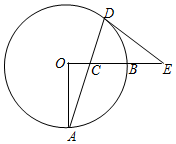 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8. 平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④.
平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④. 如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.
如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.