题目内容
12.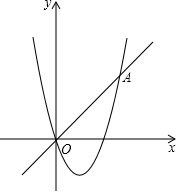 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.(1)求二次函数表达式;
(2)直线x=m和x=m+2分别交线段AO于C、D,交二次函数y=x2+bx+c的图象于点E、F,当m为何值时,四边形CEFD是平行四边形;
(3)在第(2)题的条件下,设CE与x轴的交点为M,将△COM绕点O顺时针旋转得到△C′OM′,当C′、M′、F三点第一次共线时,求线段C′D的长.
分析 (1)利用待定系数法求抛物线解析式;
(2)利用一次函数和二次函数图象上点的坐标特征,设C(m,m),D(m+2,m+2),则E(m,m2-3m),F(m+2,m2+m-2),根据平行四边形的判定得到,当CE=DF时,四边形CEFD为平行四边形,即m+2-(m2-3m)=m+2-(m2+m-2),然后解方程求出m的值;
(3)如图,利用条件画出几何图形,再作C′H⊥x轴于H,当m=1时,C(1,1),D(3,3),F(3,0),即F点为抛物线与x轴的一个交点,易得OM=CM=1,OC=$\sqrt{2}$,根据旋转的性质得OM′=C′M′=1,∠OM′C′=∠OMC=90°,再利用勾股定理计算出FM′=2$\sqrt{2}$,则FC′=2$\sqrt{2}$-1,接着证明△FHC′∽△FM′O,利用相似比可计算出FH=$\frac{8-2\sqrt{2}}{3}$,C′H=$\frac{2\sqrt{2}-1}{3}$,所以OH=OF-FH=$\frac{1+2\sqrt{2}}{3}$,于是得到C′点的坐标,然后利用两点间的距离公式可计算出线段C′D的长.
解答 解: (1)把(0,0),A(4,4)代入y=x2+bx+c得$\left\{\begin{array}{l}{c=0}\\{16+4b+c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-3}\\{c=0}\end{array}\right.$,
(1)把(0,0),A(4,4)代入y=x2+bx+c得$\left\{\begin{array}{l}{c=0}\\{16+4b+c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-3}\\{c=0}\end{array}\right.$,
所以抛物线解析式为y=x2-3x;
(2)设C(m,m),D(m+2,m+2),
则E(m,m2-3m),F[m+2,(m+2)2-3(m+2)],
即F(m+2,m2+m-2),
∵CE∥DF,
∴当CE=DF时,四边形CEFD为平行四边形,即m+2-(m2-3m)=m+2-(m2+m-2),解得m=1,
即当m为1时,四边形CEFD是平行四边形;
(3)如图,作C′H⊥x轴于H,
当m=1时,C(1,1),D(3,3),F(3,0),即F点为抛物线与x轴的一个交点,
∴OM=CM=1,OC=$\sqrt{2}$,
∵△COM绕点O顺时针旋转得到△C′OM′,
∴OM′=C′M′=1,∠OM′C′=∠OMC=90°,
在Rt△OM′F中,FM′=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
∴FC′=2$\sqrt{2}$-1,
∵∠C′FH=OFM′,
∴△FHC′∽△FM′O,
∴$\frac{C′H}{OM′}$=$\frac{FH}{FM′}$=$\frac{FC′}{FO}$,即$\frac{C′H}{1}$=$\frac{FH}{2\sqrt{2}}$=$\frac{2\sqrt{2}-1}{3}$,
∴FH=$\frac{8-2\sqrt{2}}{3}$,C′H=$\frac{2\sqrt{2}-1}{3}$,
∴OH=OF-FH=$\frac{1+2\sqrt{2}}{3}$,
∴C′($\frac{1+2\sqrt{2}}{3}$,$\frac{1-2\sqrt{2}}{3}$),
∴C′D=$\sqrt{(\frac{1+2\sqrt{2}}{3}-3)^{2}+(\frac{1-2\sqrt{2}}{3}-3)^{2}}$=4.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、旋转的性质和平行四边形的判定;会利用待定系数法求二次函数的解析式;灵活运用相似三角形的判定方法和性质;理解坐标与图形性质,记住两点间的距离公式.

| A. |  | B. |  | C. |  | D. |  |
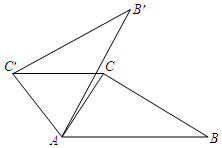 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
 如果将棱长相等的小正方体按如图的方式摆放,从上到下依次为第一层,第二层,第三层,…,那么第10层的小正方体的个数是55.
如果将棱长相等的小正方体按如图的方式摆放,从上到下依次为第一层,第二层,第三层,…,那么第10层的小正方体的个数是55.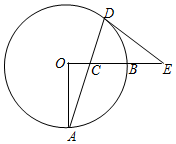 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.