题目内容
15.先化简,再求值:(1)已知分式$\frac{{a}^{2}+4{b}^{2}+4ab}{{a}^{2}-4{b}^{2}}$,其中a=3,b=$\frac{1}{2}$;
(2)已知$\frac{a-b}{ab}=-2$,求$\frac{2a+ab-2b}{a-ab-b}$的值.
分析 (1)原式变形后,约分得到最简结果,把a与b的值代入计算即可求出值;
(2)原式结合变形后,将已知等式整理后代入计算即可求出值.
解答 解:(1)原式=$\frac{(a+2b)^{2}}{(a+2b)(a-2b)}$=$\frac{a+2b}{a-2b}$,
当a=3,b=$\frac{1}{2}$时,原式=2;
(2)∵$\frac{a-b}{ab}$=-2,
∴a-b=-2ab,
则原式=$\frac{2(a-b)+ab}{a-b-ab}$=$\frac{-4ab+ab}{-2ab-ab}$=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.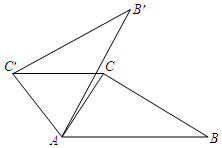 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
 如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.
如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.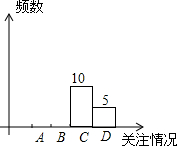 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.