题目内容
13.下列命题中,真命题的个数是( )(1)平行四边形的对角线互相平分
(2)菱形的对角线互相垂直平分
(3)对角线相等的四边形是矩形
(4)对角线互相垂直的四边形是菱形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据平行四边形的性质对(1)进行判断;根据菱形的性质对(2)进行判断;根据矩形的判定方法对(3)进行判断;根据菱形的判定方法对(4)进行判断.
解答 解:平行四边形的对角线互相平分,所以(1)正确;
菱形的对角线互相垂直平分,所以(2)正确;
对角线相等的平行四边形是矩形,所以(3)正确;
对角线互相垂直的平行四边形是菱形,所以④错误.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
相关题目
4.若盒子里装有质地均匀的红、黄、蓝、白四中不同颜色的球各一个,摇匀后,小明从中抽取白色球的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
1.若ax=4,ay=7,则a2y+x的值为( )
| A. | 196 | B. | 112 | C. | 56 | D. | 45 |
8. 如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
 如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )| A. | 15° | B. | 30° | C. | 60° | D. | 120° |
18.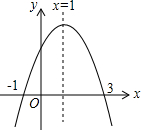 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ②④ |
5.下列命题中,是真命题的是( )
| A. | 有两条边相等的三角形是等腰三角形 | |
| B. | 同位角相等 | |
| C. | 如果|a|=|b|,那么a=b | |
| D. | 面积相等的两个三角形全等 |
3. 如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
 如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )| A. | 18° | B. | 26° | C. | 36° | D. | 72° |