题目内容
10.(1)若一次函数y=kx+b(k≠0)的图象经过点A(1,1)点B(2,3),求这个函数的解析式;(2)若一直线与此一次函数的图象交于(-2,m)点,且与y轴的交点的坐标为(0,5),求这条直线的解析式.
分析 (1)根据点A、B的坐标利用待定系数法即可求出这个函数的解析式;
(2)根据一次函数图象上点的坐标特征即可求出两直线的交点坐标,再根据点的坐标利用待定系数法即可求出这条直线的解析式.
解答 解:(1)将A(1,1)、B(2,3)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=1}\\{2k+b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴这个函数的解析式为y=2x-1.
(2)设这条直线的解析式为y=mx+n(m≠0),
当x=-2时,y=2x-1=-5,
∴两直线的交点坐标为(-2,-5).
将(-2,-5)、(0,5)代入y=mx+n,
$\left\{\begin{array}{l}{-2m+n=-5}\\{n=5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=5}\\{n=5}\end{array}\right.$,
∴这条直线的解析式为y=5x+5.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,能够熟练运用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
18. 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
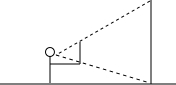 如图,一个人拿着一把厘米刻度尺,站山在距电线杆30m的地方,把甲臂向前伸直,刻度尺竖直,尺上0-12cm这一段恰好遮住电线杆.若手臂的长为60cm.求电线杆的高度.
如图,一个人拿着一把厘米刻度尺,站山在距电线杆30m的地方,把甲臂向前伸直,刻度尺竖直,尺上0-12cm这一段恰好遮住电线杆.若手臂的长为60cm.求电线杆的高度.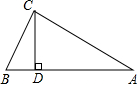 已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形△ABC∽△ACD.
已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形△ABC∽△ACD. 如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.
如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.