题目内容
18.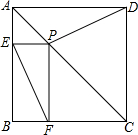 如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | 6 |
分析 根据正方形的四条边都相等可得AB=AD,正方形的对角线平分一组对角可得∠BAC=∠DAC=45°,然后利用“边角边”证明△ABP和△ADP全等,根据全等三角形对应边相等证明即可;求出四边形BFPE是矩形,根据矩形的对角线相等可EF=PB.即可.
解答 解:如图,连接PB,
在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
在△ABP和△ADP中,$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAC}\\{AP=AP}\end{array}\right.$
∴△ABP≌△ADP(SAS),
∴BP=DP;
∵PE⊥AB,PF⊥BC,∠ABC=90°,
∴四边形BFPE是矩形,
∴EF=PB,
∴EF=DP=3,
故选B
点评 本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,熟记正方形的性质得到三角形全等的条件是解题的关键

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
5.若实数a、b、c满足a+b+c=0且a<b<c,则一次函数y=ax+c的图象一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6. 如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
 如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | 4-2$\sqrt{3}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ |
 (2)
(2)
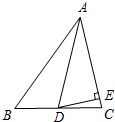 如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°. 如图,一种拉杆式旅行箱的示意图,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,其直径为10cm,⊙A与水平地面切于点D,过A作AE∥DM.当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面(40$\sqrt{3}$+5)cm,求此时拉杆箱与水平面AE所成角∠CAE的大小及点B到水平地面的距离.
如图,一种拉杆式旅行箱的示意图,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,其直径为10cm,⊙A与水平地面切于点D,过A作AE∥DM.当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面(40$\sqrt{3}$+5)cm,求此时拉杆箱与水平面AE所成角∠CAE的大小及点B到水平地面的距离.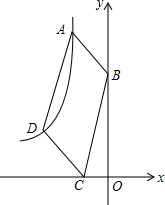 如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标.
如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标.