题目内容
14．
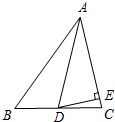如图，在△ABC中，AD是角平分线，∠B=45°，∠C=76°．（1）求∠ADB和∠ADC的度数；
（2）若DE⊥AC，求∠EDC的度数．
分析 （1）根据三角形的内角和和三角形的外角的性质即可得到结论；
（2）根据三角形的内角和即可得到结论．
解答 解：（1）∵∠B=45°，∠C=76°，
∴∠BAC=59°，
∵AD是角平分线，
∴∠BAD=∠CAD=29.5°，
∴∠ADB=∠B+∠BAD=74.5°，∠ADC=105.5°；
（2）∵DE⊥AC，
∴∠CED=90°，
∴∠EDC=90°-∠C=14°．
点评 本题考查了三角形的角平分线、中线和高的相关知识；利用三角形的内角和求得∠BAC的度数是正确解答本题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
C. 
D. 
，则该扇形圆心角是（ ）
18．
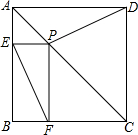如图，在正方形ABCD中，点P在AC上，PE⊥AB，PF⊥BC，垂足分别为E、F，EF=3，则PD的长为（ ）
如图，在正方形ABCD中，点P在AC上，PE⊥AB，PF⊥BC，垂足分别为E、F，EF=3，则PD的长为（ ）| A． | 2 | B． | 3 | C． | $\frac{3}{2}$ | D． | 6 |
如图，在△ABC中，点D是边BC中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点P在边AB上，EF∥BC．