题目内容
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
[操作发现]
在等腰三角形ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图4247(1),其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论:①AF=AG=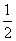 AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.其中正确的是____________(填序号即可).
AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.其中正确的是____________(填序号即可).
[数学思考]
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图4247(2),M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程.
[类比探索]
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图4247(3),M是BC的中点,连接MD和ME,试判断△MED的形状.
答:____________________.
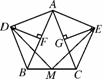
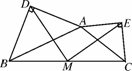
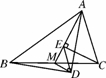
(1) (2) (3)
解:[操作发现]①②③④
[数学思考]MD=ME,MD⊥ME.证明如下:
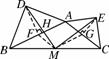
图18
①MD=ME.
如图18,分别取AB,AC的中点F,G,连接DF,MF,MG,EG,
∵M是BC的中点,
∴MF∥AC,MF=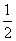 AC.
AC.
又∵EG是等腰直角三角形AEC斜边上的中线,
∴EG⊥AC,且EG=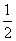 AC.
AC.
∴MF=EG.
同理可证DF=MG.
∵MF∥AC,
∴∠MFA+∠BAC=180°.
同理可得∠MGA+∠BAC=180°.
∴∠MFA=∠MGA.
又∵EG⊥AC,∴∠EGA=90°.
同理可得∠DFA=90°.
∴∠MFA+∠DFA=∠MGA+∠EGA,
即∠DFM=∠MGE.又MF=EG,DF=MG,
∴△DFM≌△MGE(SAS).∴MD=ME.
②MD⊥ME.
如图18,设MD与AB交于点H,
∵AB∥MG,∴∠DHA=∠DMG.
又∵∠DHA=∠FDM+∠DFH,
即∠DHA=∠FDM+90°.
∵∠DMG=∠DME+∠GME,∴∠DME=90°.
即MD⊥ME.
[类比探究]等腰直角三角形

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案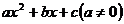 中的两项,配成完全平方式的过程叫配方.例如
中的两项,配成完全平方式的过程叫配方.例如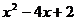 有3种形式的配方:①选取二次项和一次项配方:
有3种形式的配方:①选取二次项和一次项配方: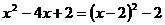 ;②选取二次项和常数项配方:
;②选取二次项和常数项配方: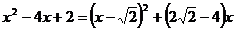 ,或
,或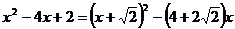 ;
;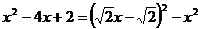 .
.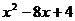 的两种不同形式的配方;
的两种不同形式的配方;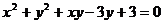 ,求
,求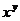 的值.
的值. 的4个外角,若
的4个外角,若 =120°,求∠1+∠2+∠3+∠4的度数
=120°,求∠1+∠2+∠3+∠4的度数
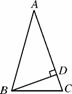 图4236
图4236

 B.
B. C.-3 D.
C.-3 D.
 =
= 的解是( )
的解是( ) D.x=-2
D.x=-2