题目内容
2.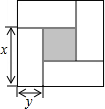 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )| A. | x+y=7 | B. | x-y=2 | C. | x2-y2=4 | D. | 4xy+4=49 |
分析 分别根据大正方形边长、小正方形边长的不同表示可判断A、B,由A、B结论利用平方差公式可判断C,根据大正方形面积的整体与组合的不同表示可判断D.
解答 解:A、因为正方形图案的边长7,同时还可用(x+y)来表示,故此选项正确;
B、中间小正方形的边长为2,同时根据长方形长宽也可表示为x-y,故此选项正确;
C、根据A、B可知x+y=7,x-y=2,则x2-y2=(x+y)(x-y)=14,故此选项错误;
D、因为正方形图案面积从整体看是49,从组合来看,可以是(x+y)2,还可以是(4xy+4),即4xy+4=49,故此选项正确;
故选:C.
点评 本题主要考查根据数形结合列二元一次方程的能力,解答需结合图形,利用等式的变形来解决问题.

练习册系列答案
相关题目
11.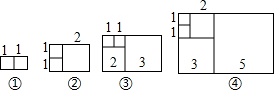 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )| A. | 168 | B. | 170 | C. | 178 | D. | 188 |
12. 如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
 如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )
如图,直线a,b被直线c所截,a∥b,若∠1=75°,则∠2的度数为( )| A. | 15° | B. | 75° | C. | 105° | D. | 无法确定 |
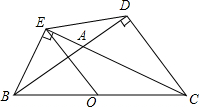 如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.
如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE. 如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.
如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.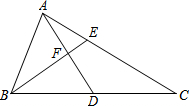 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.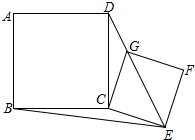 将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.
将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.