题目内容
7.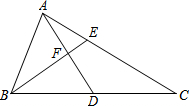 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.
分析 根据ASA证得△AFB≌△DFB,得出AB=BD,AF=FD=$\frac{1}{2}$AD=4,根据勾股定理求得BD,根据三角形面积公式求得AG,然后根据勾股定理即可求得.
解答 解:∵AD⊥BE,
∴∠AFB=∠DFB=90°,
在△AFB和△DFB中
$\left\{\begin{array}{l}{∠AFB=∠DFB}\\{BF=BF}\\{∠ABF=∠DBF}\end{array}\right.$
∴△AFB≌△DFB,
∴AB=BD,AF=FD=$\frac{1}{2}$AD=4,
∴AB=BD=$\sqrt{B{F}^{2}+D{F}^{2}}$=$\sqrt{{5}^{2}+{4}^{2}}$=$\sqrt{41}$,
∵BD=DC,
∴BC=2$\sqrt{41}$,
作AG⊥BC于G,
∵S△ABD=$\frac{1}{2}$BD•AG=$\frac{1}{2}$AD•BF,
∴AG=$\frac{AD•BF}{BD}$=$\frac{8×5}{\sqrt{41}}$=$\frac{40}{\sqrt{41}}$,
∴DG=$\sqrt{A{D}^{2}-A{G}^{2}}$=$\sqrt{{8}^{2}-\frac{4{0}^{2}}{41}}$=$\frac{32}{\sqrt{41}}$,
∴CG=$\frac{32}{\sqrt{41}}$+$\sqrt{41}$=$\frac{73}{\sqrt{41}}$
∴AC=$\sqrt{A{G}^{2}+C{G}^{2}}$=$\sqrt{\frac{4{0}^{2}}{41}+\frac{7{3}^{2}}{41}}$=13;
故答案为:13.
点评 本题考查了三角形全等的判定和性质,勾股定理的应用,作出辅助线构建直角三角形是解题的关键.

(1)在一个变化过程中,允许出现多个变量和常量;
(2)变量就是变量,它不可以转化为常量;
(3)变量和常量是相对而言的,在一定条件下可以相互转化;
(4)在一个变化过程中,变量只有2个,常量可以没有,也可能有多个.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
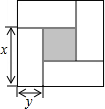 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )| A. | x+y=7 | B. | x-y=2 | C. | x2-y2=4 | D. | 4xy+4=49 |
| A. | 4(x+200-1)=5(x-1) | B. | 4(x+200)=5(x-1) | C. | 4(x+200-1)=5x | D. | 4(x+200)=5x |
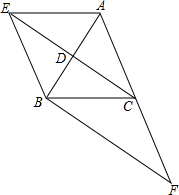 已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.
已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.