题目内容
14.简便计算:(2+1)(22+1)(24+1)(28+1)×…×(2128+1).分析 根据平方差公式,可得答案.
解答 解:原式=(2-1)(2+1)(22+1)(24+1)(28+1)×…×(2128+1)
=(22-1)(22+1)(24+1)(28+1)×…×(2128+1)
=(24-1)(28+1)×…×(2128+1)
=(28-1)(28+1)×…×(2128+1)
=(2128-1)(2128+1)
=2256-1.
点评 本题考查了平方差公式,乘以(2-1)得出平方差公式是解题关键.

练习册系列答案
相关题目
4.以下元素对应相等,不能判定两个三角形全等的是( )
| A. | 三个角 | B. | 两边及夹角 | C. | 两角和一边 | D. | 三条边 |
5.设函数y=x2+2kx+k-1(k为常数),下列说法正确的是( )
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | k取不同的值时,二次函数y的顶点始终在同一条直线上 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
6.如图所示,下列图案均是由完全相同的“太阳型”图标按一定的规律拼搭而成:第1个图案需要2个图标,第2个图案需要4个图标,第3个图案需要7个图标,…,按此规律,第n个图案需要图标的个数是n+2n-1.


2.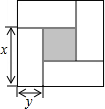 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )| A. | x+y=7 | B. | x-y=2 | C. | x2-y2=4 | D. | 4xy+4=49 |
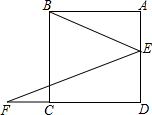 如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.