题目内容
4.下列对方程x2=0的根描述正确的是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 无实数根 |
分析 先计算判别式的值得到△=0-4×1×0=0,然后根据判别式的意义进行判断.
解答 解:△=0-4×1×0=0,
∴方程有两个相等的实数根.
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
14.下列四个算式中,有一个算式与其他三个算式的计算结果符号不同,则该算式是( )
| A. | (-2013)2 | B. | -20132 | C. | (-2013)3 | D. | -|-2013| |
15.下列关于二次函数y=-(x-3)2+$\frac{1}{2}$的说法,错误的是( )
| A. | 其对称轴为x=3 | B. | 其图象的顶点坐标为(3,$\frac{1}{2}$) | ||
| C. | 其图象开口方向向下 | D. | 其图象与y轴的交点坐标为(0,$\frac{1}{2}$) |
9. 如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
 如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )| A. | 26° | B. | 16° | C. | 23° | D. | 20° |
16.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
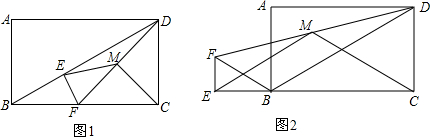
 已知:如图,E,F是?ABCD的对角线AC上的两点,BE∥DF,求证:AF=CE.
已知:如图,E,F是?ABCD的对角线AC上的两点,BE∥DF,求证:AF=CE.