题目内容
13.设b为正整数,a为实数,记M=a2-4ab+5b2+2a-2b+$\frac{11}{4}$,在a,b变动的情况下,求M可能取得的最小整数值.并求出M取得最小整数值时a、b的值.分析 根据配方法把M进行变形,根据b为正整数,求出M可能取得的最小整数值,把M的最小值代入配方后的式子,求出a、b的值.
解答 解:M=a2-4ab+5b2+2a-2b+$\frac{11}{4}$
=(a-2b)2+2(a-2b)+1+b2+2b+$\frac{3}{4}$
=(a-2b+1)2+(b+1)2+$\frac{3}{4}$,
∵b为正整数,
∴M≥$\frac{19}{4}$,M可能取得的最小整数值是5,
(a-2b+1)2+(b+1)2+$\frac{3}{4}$=5,
(a-2b+1)2+(b+1)2=$\frac{17}{4}$,
∵b为正整数,∴b+1=2,
(a-2b+1)2=$\frac{1}{4}$,
a=$\frac{1}{2}$或a=$\frac{3}{2}$,
∴b=1,a=$\frac{1}{2}$或a=$\frac{3}{2}$.
点评 本题考查的是配方法的应用和非负数的性质,掌握配方法的步骤和非负数的性质是解题的关键.

练习册系列答案
相关题目
4.下列对方程x2=0的根描述正确的是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 无实数根 |
2.两个相似三角形的面积和为78cm2,一组对应边的边长分别为2cm和3cm,则较大三角形的面积为( )
| A. | 44.8cm | B. | 42cm | C. | 52cm | D. | 54cm |
14.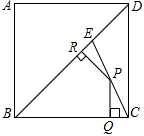 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\frac{8}{3}$ |
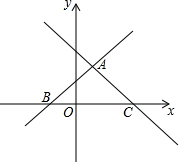 如图,在平面直角坐标系xOy中,直线y=x+1与y=-$\frac{3}{4}$x+3交于点A,且分别交x轴于点B和点C.
如图,在平面直角坐标系xOy中,直线y=x+1与y=-$\frac{3}{4}$x+3交于点A,且分别交x轴于点B和点C.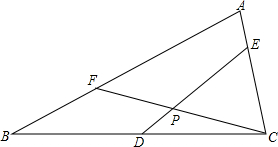 如图,已知3AE=EC,2BF=AF,D为BC的中点,求EP:DP的值.
如图,已知3AE=EC,2BF=AF,D为BC的中点,求EP:DP的值.