题目内容
1.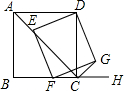 如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.
分析 (1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEM≌△FEM,则有DE=EF即可;
(2)同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC=4;
(3)由正方形的性质得到∠DAE=45°,表示出AM=EM,再表示出DM,再用勾股定理求出DE2.
解答 解:(1)如图,作EM⊥BC,EN⊥CD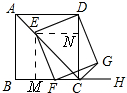
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
在△DEN和△FEM中,
$\left\{\begin{array}{l}{∠DNE=∠FME}\\{EN=EM}\\{∠DEN=∠FEM}\end{array}\right.$,
∴△DEN≌△FEM,
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为4,
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
∴△ADE≌△CDG,
∴AE=CG.
∴CE+CG=CE+AE=AC=$\sqrt{2}$AB=$\sqrt{2}$×2$\sqrt{2}$=4,
(3)如图,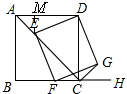
∵正方形ABCD中,AB=2$\sqrt{2}$,
∴AC=4,
过点E作EM⊥AD,
∴∠DAE=45°,
∵AE=x,
∴AM=EM=$\frac{\sqrt{2}}{2}$x,
在Rt△DME中,DM=AD-AM=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x,EM=$\frac{\sqrt{2}}{2}$x,
根据勾股定理得,DE2=DM2+EM2=(2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=x2-4x+8,
∵四边形DEFG为正方形,
∴S=S正方形DEFG=DE2=x2-4x+8.
点评 此题是四边形综合题,主要考查了正方形的性质,矩形的性质,矩形的判定,三角形的全等的性质和判定,勾股定理,解本题的关键是作出辅助线,判断三角形全等.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 “斗地主”是常见的一种游戏,一副扑克牌除大、小王外共有四种花色,每种花色从小到大共有牌面为3、4、5、6、7、8、9、10、J、Q、K、A、2的牌各一张(如图),现甲、乙、丙玩“斗地主”游戏,
“斗地主”是常见的一种游戏,一副扑克牌除大、小王外共有四种花色,每种花色从小到大共有牌面为3、4、5、6、7、8、9、10、J、Q、K、A、2的牌各一张(如图),现甲、乙、丙玩“斗地主”游戏,
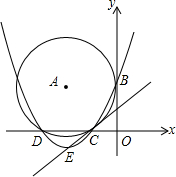 如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).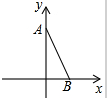 如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).
如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).