题目内容
12.材料:分母中含有未知数的不等式叫分式不等式,如:$\frac{2x}{x+1}$>0;$\frac{x+3}{x-1}$<0等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则$\frac{a}{b}$>0;若a<0,b<0,则$\frac{a}{b}$>0;
(2)若a>0,b<0,则$\frac{a}{b}$<0;若a<0,b>0,则$\frac{a}{b}$<0.
反之:(1)若$\frac{a}{b}$>0,则$\left\{\begin{array}{l}{a>0}\\{b>0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b<0}\end{array}\right.$
(2)若$\frac{a}{b}$<0,则$\left\{\begin{array}{l}{a>0}\\{b<0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$.
根据上述规律,求不等式$\frac{x+1}{x-3}$>0的解集.
分析 由题意知若$\frac{a}{b}$<0,则$\left\{\begin{array}{l}{a>0}\\{b<0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$;将不等式$\frac{x+1}{x-3}$>0转化为$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$或$\left\{\begin{array}{l}{x+1<0}\\{x-3<0}\end{array}\right.$,分别求每个不等式组的解集即可.
解答 解:根据题意若$\frac{a}{b}$<0,则$\left\{\begin{array}{l}{a>0}\\{b<0}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$,
由不等式$\frac{x+1}{x-3}$>0得:$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$或$\left\{\begin{array}{l}{x+1<0}\\{x-3<0}\end{array}\right.$,
解不等式组$\left\{\begin{array}{l}{x+1>0}\\{x-3>0}\end{array}\right.$得:x>3,
解不等式组$\left\{\begin{array}{l}{x+1<0}\\{x-3<0}\end{array}\right.$得:x<-1,
故不等式$\frac{x+1}{x-3}$>0的解集为:x<-1或x>3,
故答案为:$\left\{\begin{array}{l}{a>0}\\{b<0}\end{array}\right.$,$\left\{\begin{array}{l}{a<0}\\{b>0}\end{array}\right.$.
点评 本题主要考查解不等式、不等式组的能力,将原不等式转化为两个不等式组是解题的关键.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | 42.31×106 | B. | 4.231×105 | C. | 42.31×108 | D. | 42.31×107 |
| A. | x | B. | $\frac{1}{x+2}$ | C. | $\frac{x}{x+2}$ | D. | x+2 |
 已知直线y=2x+6,解答下列问题:
已知直线y=2x+6,解答下列问题: 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点D在AB上,连接AC,求证:△AOC≌△BOD.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点D在AB上,连接AC,求证:△AOC≌△BOD.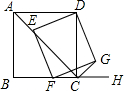 如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.