题目内容
6.若关于x的一元二次方程x2-(2m+1)x+m2+2m=0有实数根,则m的取值范围是m≤$\frac{1}{4}$.分析 由方程有实数根可得知b2-4ac≥0,代入数据即可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:由已知得:b2-4ac=[-(2m+1)]2-4(m2+2m)≥0,
即1-4m≥0,解得:m≤$\frac{1}{4}$.
故答案为:m≤$\frac{1}{4}$.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是得出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,由根的个数结合根的判别式得出不等式(方程或不等式组)是关键.

练习册系列答案
相关题目
15.下列各数中最小的数是( )
| A. | -π | B. | -3 | C. | -$\sqrt{5}$ | D. | 0 |
 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点D在AB上,连接AC,求证:△AOC≌△BOD.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点D在AB上,连接AC,求证:△AOC≌△BOD.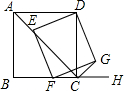 如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
如图,已知四边形ABCD为正方形,AB=2$\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.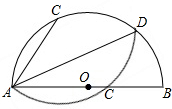 如图,半圆O的直径AB=10cm,D为$\widehat{AB}$上一点,C为$\widehat{AD}$上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为4$\sqrt{5}$cm.
如图,半圆O的直径AB=10cm,D为$\widehat{AB}$上一点,C为$\widehat{AD}$上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为4$\sqrt{5}$cm. 如图,菱形ABCD的对角线交于点O,AC=16cm,BD=12cm.
如图,菱形ABCD的对角线交于点O,AC=16cm,BD=12cm.