题目内容
18.方程2x2-xy-3x+3y+2006=0的正整数解(x,y)为(4,2026);(8,442);(16,19);(34,136);(68,170);(158,332);(406,820);(2018,4040).分析 先将原方程化成(x-3)(y-3-2x)=5×13×31,再分八种情况进行讨论计算即可得出结论.
解答 解:∵2x2-xy-3x+3y+2006=0,
∴(2x2-6x)-(xy-3y)+(3x+9)=-2015,
∴(x-3)(2x-y+3)=-2015,
∴(x-3)(y-3-2x)=5×13×31,
∴①$\left\{\begin{array}{l}{x-3=1}\\{y-3-2x=2015}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=2026}\end{array}\right.$,即:(x,y)=(4,2026);
②$\left\{\begin{array}{l}{x-3=5}\\{y-3-2x=403}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=8}\\{y=422}\end{array}\right.$,即:(x,y)=(8,442);
③$\left\{\begin{array}{l}{x-3=13}\\{y-3-2x=155}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=16}\\{y=190}\end{array}\right.$,即:(x,y)=(16,19);
④$\left\{\begin{array}{l}{x-3=31}\\{y-3-2x=65}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=34}\\{y=136}\end{array}\right.$,即:(x,y)=(34,136);
⑤$\left\{\begin{array}{l}{x-3=65}\\{y-3-2x=31}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=68}\\{y=170}\end{array}\right.$,即:(x,y)=(68,170);
⑥$\left\{\begin{array}{l}{x-3=155}\\{y-3-2x=13}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=158}\\{y=332}\end{array}\right.$,即:(x,y)=(158,332);
⑦$\left\{\begin{array}{l}{x-3=403}\\{y-3-2x=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=406}\\{y=820}\end{array}\right.$,即:(x,y)=(406,820);
⑧$\left\{\begin{array}{l}{x-3=2015}\\{y-3-2x=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2018}\\{y=4040}\end{array}\right.$,即:(x,y)=(2018,4040);
故答案为:(4,2026);(8,442);(16,19);(34,136);(68,170);(158,332);(406,820);(2018,4040).
点评 此题是非一次不定方程(组),主要考查了一元二次方程的整数根与有理数根,以及不等式的化简,因式分解,分解质因数解本题的关键是把原方程化成(x-3)(y-3-2x)=2015.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 如图,数轴上A,B两点之间表示的整数共有( )
如图,数轴上A,B两点之间表示的整数共有( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
 如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=8.求△AEG周长.
如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=8.求△AEG周长. 如图,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为( )
如图,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为( )



 如图,在△ABC中,∠ABC=∠ACB,AC为直径的⊙O分别交AB、BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.
如图,在△ABC中,∠ABC=∠ACB,AC为直径的⊙O分别交AB、BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.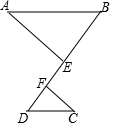 如图,已知AB∥DC,点E、F在线段BD上,AB=2DC,BE=2DF.
如图,已知AB∥DC,点E、F在线段BD上,AB=2DC,BE=2DF.