题目内容
2.化简||x-1|-2|分析 根据题意,分4种情况:①当x≤-1时;②当-1<x≤1时;③当1<x≤3时;④当x>3时;然后根据绝对值的求法,以及整数加减法的运算方法,求出算式||x-1|-2|的值是多少即可.
解答 解:①当x≤-1时,
||x-1|-2|
=|1-x-2|
=-1-x;
②当-1<x≤1时,
||x-1|-2|
=|1-x-2|
=1+x;
③当1<x≤3时,
||x-1|-2|
=|x-1-2|
=3-x;
④当x>3时,
||x-1|-2|
=|x-1-2|
=x-3.
综上,可得||x-1|-2|=$\left\{\begin{array}{l}{-1-x(x≤-1)}\\{1+x(-1<x≤1)}\\{3-x(1<x≤3)}\\{x-3(x>3)}\end{array}\right.$.
点评 此题主要考查了整式的加减运算,要熟练掌握,解答此题的关键是要明确:①整式的加减的实质就是去括号、合并同类项.一般步骤是:先去括号,然后合并同类项.②去括号时,要注意两个方面:一是括号外的数字因数要乘括号内的每一项;二是当括号外是“-”时,去括号后括号内的各项都要改变符号.此题还考查了绝对值的非负性质和求法的应用,考查了分类讨论思想的应用,要熟练掌握.

练习册系列答案
相关题目
14.式子|x-1|+3取最小值时,x等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
11.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若k是方程3x+1=7的解,则4k+3的值是( )
| A. | 11 | B. | -11 | C. | 17 | D. | -7 |
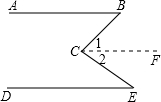 如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.
如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.