题目内容
15.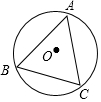 如图△ABC是⊙O的内接三角形,∠BAC=45°,BC=5,则⊙O的直径为5$\sqrt{2}$.
如图△ABC是⊙O的内接三角形,∠BAC=45°,BC=5,则⊙O的直径为5$\sqrt{2}$.
分析 首先作⊙O的直径CD,连接BD,可得∠CBD=90°,由已知条件得出△BCD是等腰直角三角形,得出CD=$\sqrt{2}$BC=5$\sqrt{2}$即可.
解答  解:如图,作⊙O的直径CD,连接BD,则∠CBD=90°,
解:如图,作⊙O的直径CD,连接BD,则∠CBD=90°,
∵∠D=∠BAC=45°,
∴△BCD是等腰直角三角形,
∴CD=$\sqrt{2}$BC=5$\sqrt{2}$,
即⊙O的直径为5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 此题考查了圆周角定理、等腰直角三角形的性质以及三角形的外接圆的综合应用,在同圆或等圆中,同弧或等弧所对的圆周角相等.解题时注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,⊙O是△ABC的外接圆,∠A=70°,则∠BOC的大小是( )
如图,⊙O是△ABC的外接圆,∠A=70°,则∠BOC的大小是( )
 如图,⊙O是△ABC的外接圆,∠A=70°,则∠BOC的大小是( )
如图,⊙O是△ABC的外接圆,∠A=70°,则∠BOC的大小是( )| A. | 30° | B. | 35° | C. | 70° | D. | 140° |
6.方程x2+2x=3的根是( )
| A. | x1=1,x2=-3 | B. | x1=-1,x2=3 | C. | x1=-1+$\sqrt{3}$,x2=-1-$\sqrt{3}$ | D. | x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$ |
3.下列说法正确的是( )
| A. | 1的平方根是1 | B. | -3是$\sqrt{(-3)^{2}}$的平方根 | ||
| C. | $\sqrt{2}$是2的平方根 | D. | -1的立方根是-1 |
10.4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | 4 | D. | -2 |
20.在平面直角坐标系中,已知点P的坐标是(3,4),点P与点Q关于y轴对称,则点Q的坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
 如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.
如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.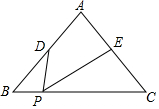 △ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4.
△ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4.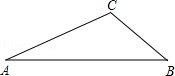 已知△ABC中,∠A=30°,AC=6.
已知△ABC中,∠A=30°,AC=6.