题目内容
18.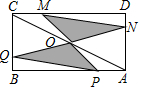 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
分析 先根据矩形的性质得出OE=$\frac{1}{2}$BC=2,OF=$\frac{1}{2}$AB=4,再设BQ=x,则由点P的速度是点Q的速度2倍,可得AP=2x,BP=8-2x,CQ=4-x,最后根据△POQ的面积=Rt△ABC的面积-△AOP的面积-△COQ的面积-△BPQ的面积,可得二次函数:y=2x2-8x+16(0≤x≤4),据此可得结论.
解答 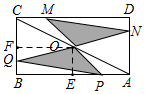 解:如图所示,过O作OE⊥AB于E,OF⊥BC于F,
解:如图所示,过O作OE⊥AB于E,OF⊥BC于F,
∵矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,
∴OE=$\frac{1}{2}$BC=2,OF=$\frac{1}{2}$AB=4,
设BQ=x,则由点P的速度是点Q的速度2倍,可得AP=2x,BP=8-2x,CQ=4-x,
∵△POQ的面积=Rt△ABC的面积-△AOP的面积-△COQ的面积-△BPQ的面积
=$\frac{1}{2}$×4×8-$\frac{1}{2}$×2x×2-$\frac{1}{2}$×(4-x)×4-$\frac{1}{2}$x(8-2x)
=x2-4x+8,
∴阴影部分面积y=2x2-8x+16(0≤x≤4),
∴当x=2时,阴影部分面积y有最小值,
根据二次函数的性质,可得阴影部分面积先减小后增大,
故选:C.
点评 本题主要考查了矩形的性质以及二次函数的性质的运用,解题时注意函数思想以及数形结合思想的运用.

练习册系列答案
相关题目
13.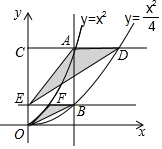 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
10.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2k≤0}\\{x+k>2}\end{array}\right.$有解,则k的取值范围为( )
| A. | k>-$\frac{2}{3}$ | B. | k>$\frac{2}{3}$ | C. | k≤$\frac{2}{3}$ | D. | k≥-$\frac{2}{3}$ |
7.下列图形中,可以是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
10.若二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(0,1),且顶点在第四象限,则s=4a+2b+c的取值范围是( )
| A. | s>-1且s≠1 | B. | s>-3且s≠1 | C. | -3<s<-1 | D. | -1<s<0 |
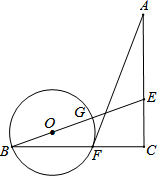 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.
如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F. 如图,O是矩形ABCD对角线的交点,BO=BE,∠AOD=120°,∠AEO=30°.
如图,O是矩形ABCD对角线的交点,BO=BE,∠AOD=120°,∠AEO=30°. 如图,菱形ABCD中,P为AB中点,∠A=60°,折叠菱形ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为75°.
如图,菱形ABCD中,P为AB中点,∠A=60°,折叠菱形ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为75°.