题目内容
已知:如图,在△ABC中,AC=AB,CD⊥AB于点D,过点A作AE⊥AC交CB的延长线于点E,EG⊥AB交AB延长线于点G.求证:
(1)EC平分∠AEG;
(2)AD=BG.
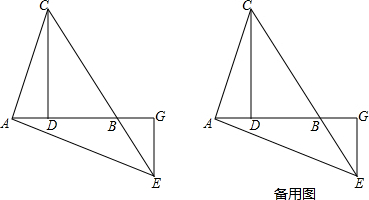
(1)EC平分∠AEG;
(2)AD=BG.

考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据等腰三角形的性质得出∠ACB=∠ABC,根据三角形内角和定理求出∠ACE+∠AEC=∠EBG+∠BEG=90°,根据∠ACB=∠ABC=∠EBG求出∠AEC=∠BEG,即可得出答案;
(2)过点B作BF⊥AE于点F,根据角平分线性质求出BF=BG,证△ACD≌△BAF,推出AD=BF即可.
(2)过点B作BF⊥AE于点F,根据角平分线性质求出BF=BG,证△ACD≌△BAF,推出AD=BF即可.
解答:证明:(1)∵AC=AB,
∴∠ACB=∠ABC,
∵AE⊥AC,EG⊥AB,
∴∠CAE=∠AGE=90°,
∴∠ACE+∠AEC=∠EBG+∠BEG=90°,
又∵∠ACB=∠ABC=∠EBG,
∴∠AEC=∠BEG,
即:EC平分∠AEG;
(2)过点B作BF⊥AE于点F,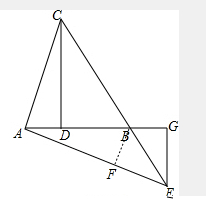
∴∠AFB=90°,
由(1)知EC平分∠AEG,
∴BF=BG,
∵CD⊥AB,
∴∠ADC=90°=∠AFB,
∴∠ACD=∠FAB,
在△ACD和△BAF中,
,
∴△ACD≌△BAF(AAS),
∴AD=BF,
∴AD=BG.
∴∠ACB=∠ABC,
∵AE⊥AC,EG⊥AB,
∴∠CAE=∠AGE=90°,
∴∠ACE+∠AEC=∠EBG+∠BEG=90°,
又∵∠ACB=∠ABC=∠EBG,
∴∠AEC=∠BEG,
即:EC平分∠AEG;
(2)过点B作BF⊥AE于点F,

∴∠AFB=90°,
由(1)知EC平分∠AEG,
∴BF=BG,
∵CD⊥AB,
∴∠ADC=90°=∠AFB,
∴∠ACD=∠FAB,
在△ACD和△BAF中,
|
∴△ACD≌△BAF(AAS),
∴AD=BF,
∴AD=BG.
点评:本题考查了三角形内角和定理,全等三角形的性质和判定,角平分线性质的应用,能综合运用性质进行推理是解此题的关键,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、不确定事件发生的概率是不确定的 |
| B、事件发生的概率可以等于事件不发生的概率 |
| C、事件发生的概率不可能等于0 |
| D、抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于2 |
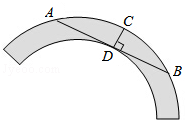 如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.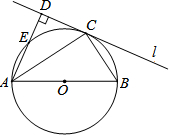 如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E.