题目内容
9.如图,AB是⊙O的直径,C、P是弧AB上两点,AB=13,AC=5,
(1)如图(1),若点P是弧AB的中点,求PB的长;
(2)如图(2),过点P作PD⊥BC于点E,交AB于点D,若$\frac{DE}{EP}$=$\frac{5}{4}$,求PC的长.
分析 (1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得;
(2)延长AC,PB交于点G,根据PD⊥BC,AC⊥BC.得到AC∥PD,得到比例式,求得CG=4,根据勾股定理求出BC的长度,得到GB的长度通过三角形相似得出结论.
解答 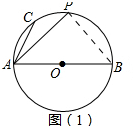 解:(1)如图(1)所示,连接PB,
解:(1)如图(1)所示,连接PB,
∵AB是⊙O的直径且P是$\widehat{AB}$的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=13,
∴PB=$\frac{AB}{\sqrt{2}}$=$\frac{13}{\sqrt{2}}$=$\frac{13\sqrt{2}}{2}$;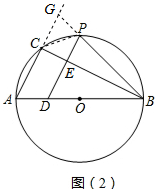 (2)如图(2)所示,延长AC,PB交于点G,
(2)如图(2)所示,延长AC,PB交于点G,
∵PD⊥BC,AC⊥BC.
∴AC∥PD,
∴$\frac{PE}{GC}$=$\frac{BE}{BC}$=$\frac{DE}{AC}$,
∴$\frac{DE}{EP}$=$\frac{AC}{GC}$=$\frac{5}{4}$,
∴CG=4,
∵AB=13,AC=5,
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=12,
∴$GB=4\sqrt{10}$,
∵∠GCB=ABP,G=∠G,
∴△GCP∽△ABG,
∴$\frac{GC}{GB}$=$\frac{CP}{AB}$,
∴CP=$\frac{13\sqrt{10}}{10}$.
点评 本题考查了圆周角的定理,垂径定理,勾股定理,等腰三角形判定和性质,相似三角形的判定和性质,作出辅助线是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知坐标原点为O,点A(2,1),将OA绕原点O顺时针旋转90°后,A的对应点A1的坐标是( )
| A. | (2,-1) | B. | (-2,1) | C. | (1,-2) | D. | (-1,2) |
18.过点A(-3,3)和点B(6,3)的直线一定( )
| A. | 垂直于x轴 | B. | 于y轴相交但不平行于x轴 | ||
| C. | 平行于x轴 | D. | 平行于y轴 |
19.使$\sqrt{x+1}$有意义的x的取值范围是( )
| A. | x≥-1 | B. | x<1 | C. | x>-1 | D. | x≤1 |
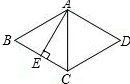 如图,菱形ABCD的边长为2,高AE平分BC,求:
如图,菱形ABCD的边长为2,高AE平分BC,求: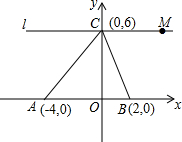 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)